Fakultät > Vorlesungen > Sommersemester 2022 > Theoretische Physik IV (Quantenmechanik)

Theoretische Physik IV (Quantenmechanik)

Dozent: Maurits W. Haverkort

Wir werden während dieser Vorlesung dem für dieses Semester geschriebenen Skript folgen. Das Skript ist in Englisch und Deutsch verfügbar. Kapitel 11 zu relativistischen Effekten, Kapitel 13 zu Response-Theorie und Abschnit 9.4 sowie die zweite Hälfte von Kapitel 7 (ab 7.5.8) sind nicht Bestandteil der Prüfung. Wir werden ungefähr eine Woche pro Kapitel verbringen. Wir gehen davon aus, dass es sich bei den ersten Kapiteln teilweise um Wiederholungen Ihrer bisherigen PEP3-Vorlesung handelt. Das Skript ist relativ umfangreich, seine Länge ergibt sich aus der detaillierten Ausarbeitung vieler Probleme innerhalb des Skripts.

Neben dem Skript gibt es viele gute Lehrbücher zur Quantenmechanik. Nachfolgend sind einige davon aufgeführt.

Die Vorlesungen finden dienstags und donnerstags von 11:15 bis 13:00 Uhr statt, beginnend am Donnerstag, den 21. April. Sie erhalten eine Hausaufgabe pro Woche und müssen diese online bis Freitagabend zurückgeben. Die Hausaufgaben werden in der Woche danach in den Tutorien besprochen. Die ersten Hausaufgaben sind am Freitag, den 29. April fällig.

Mit einiger Verzögerung werden die meisten Videos der Vorträge online verfügbar sein.

Einige andere Lehrbücher:

  • S. Gasiorowicz, Quantum Physics. Wiley, 1975, 1995, 2003.
  • J. J. Sakurai, Modern Quantum Mechanics. Cambridge University Press, 1967 - 2017.
  • D. Griffiths, Introduction to Quantum Mechanics. Cambridge Univer- sity Press, 2004, 2018.
  • A. Messiah, Quantum Mechanics I+II. North-Holland Publishing Co, 1961.
  • L. D. Landau and E. M. Lifshitz, Quantum Mechanics Non-Relativistic Theory. Elsevier, 1958, 1965, 1977.

Ein Lehrbuch zu unendlichdimensionalen Hilberträumen (für Interessierte, nicht Teil der Vorlesung):

  • B.P. Rynne and M.A. Youngson, Linear Functional Analysis. Springer (2008).

Vorlesungsinhalt

Woche 16 20. - 22. April
Kapitel 1
Woche 17 25. - 29. April
Kapitel 2+3
Woche 18 2. - 6. Mai
Kapitel 3+4
Woche 19 9. - 13. Mai
Kapitel 4+5
Woche 20 16. - 20. Mai
Kapitel 5+6
Woche 21 23. - 27. Mai
Keine Vorlesung und Übungen am Donnerstag, 26. Mai
Kapitel 6
Woche 22 30. Mai - 3. Juni
Kapitel 7
Woche 23 6. - 10. Juni
Keine Tutorials am Montag, den 6. Juni
Kapitel 7+8
Woche 24 13. - 17. Juni
Keine Vorlesung und Übungen am Donnerstag, 16. Juni
Kapitel 8
Woche 25 20. - 24. Juni
Kapitel 8+9
Woche 26 27. Juni - 1. Juli
Kapitel 9+10
Woche 27 4. Juli - 8. Juli
Kapitel 12
Woche 28 11. - 15. Juli
Kapitel 11(kurz) + 12
Woche 29 18. - 22. Juli
Zeit zum Lernen.
Treffen am Dienstag, den 19. für Fragen
Woche 30 25. - 29. Juli
Prüfung am Montag, den 25. Juli 14:15 - 17:00
Woche 31 1. - 5. August
Diskussion und Fragen zu Prüfungsergebnissen

Materialien

Mathematica-Lizenzen sind hier erhältlich.

Übungsgruppen

zum Seitenanfang
Theoretische Physik IV (Quantenmechanik)
Sommersemester 2022
Haverkort
Link zum LSF
ss22-ptp4
332 Teilnehmer/innen
Die erste Vorlesung findet am Donnerstag, den 21. April im INF227 HS1 statt. Wir werden unsere Vorlesungen über Zoom streamen, raten aber zur Präsenz.
Die Prüfung findet am Montag, den 25. Juli von 14:15 - 17:00 Uhr statt. 
Thomson Streuung elektromagnetische Strahlung an ein Wasserstoffatom
Compton Streuung elektromagnetische Strahlung an ein Wasserstoff Atom
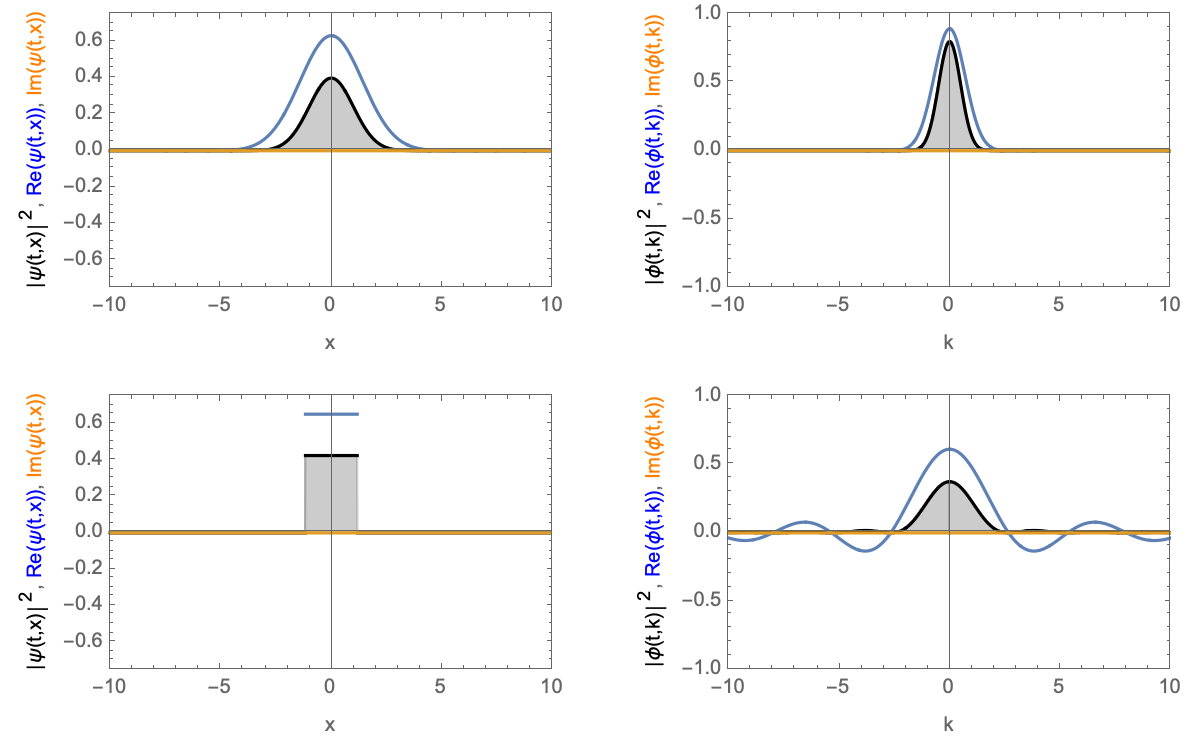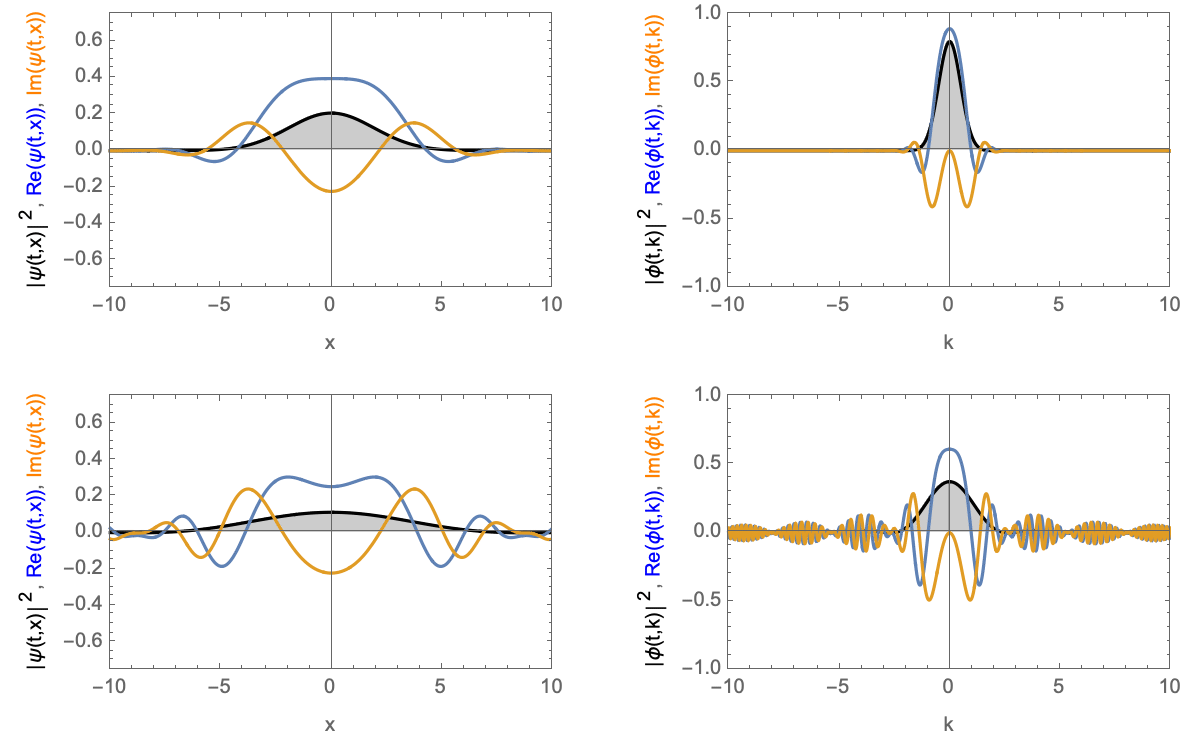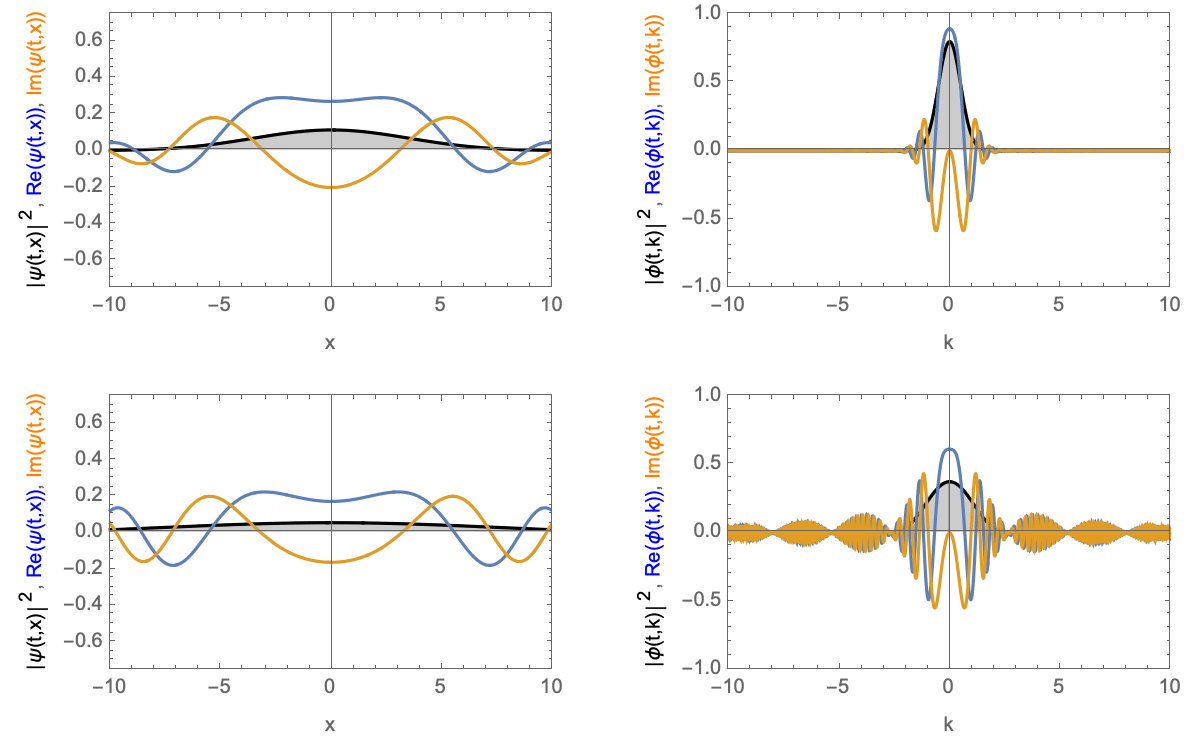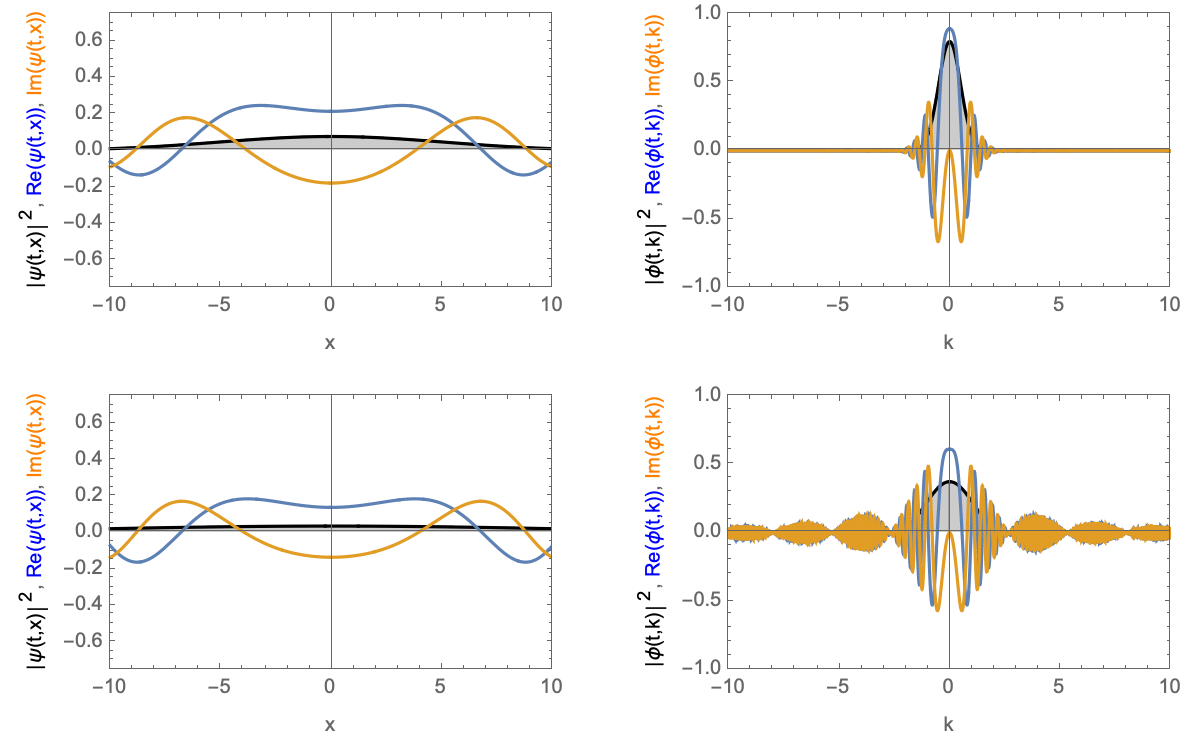Zeitentwicklung eines Wellenpakets mit Nullgeschwindigkeit. Oberes Gaußsches Wellenpaket, unteres Blockwellenpaket. Links im Realraum, rechts im Impulsraum.
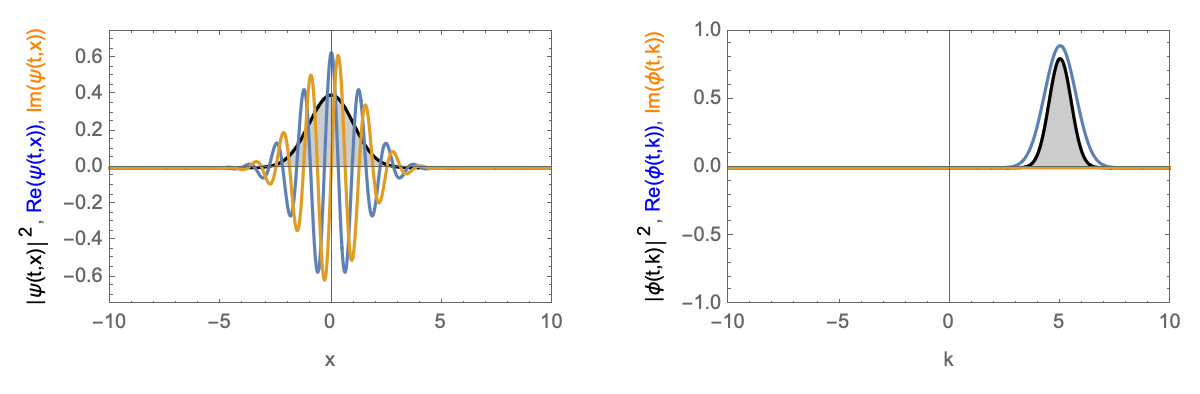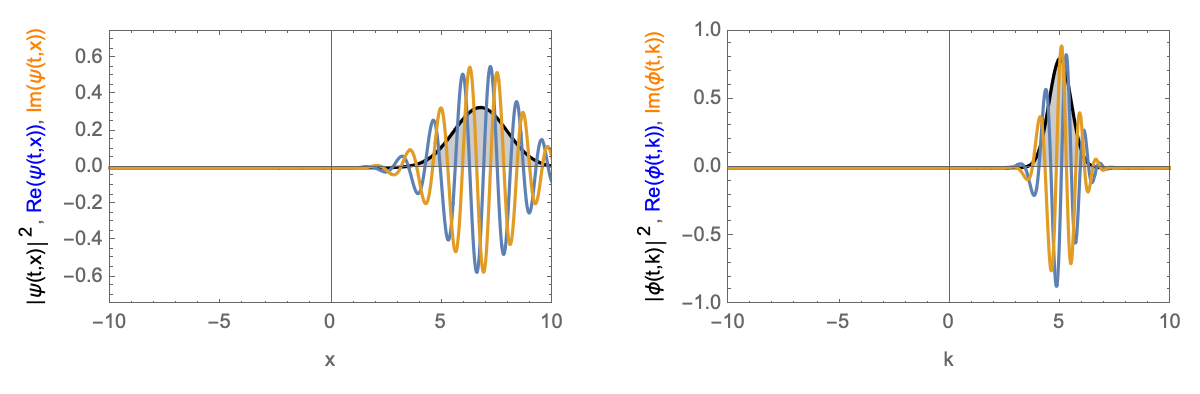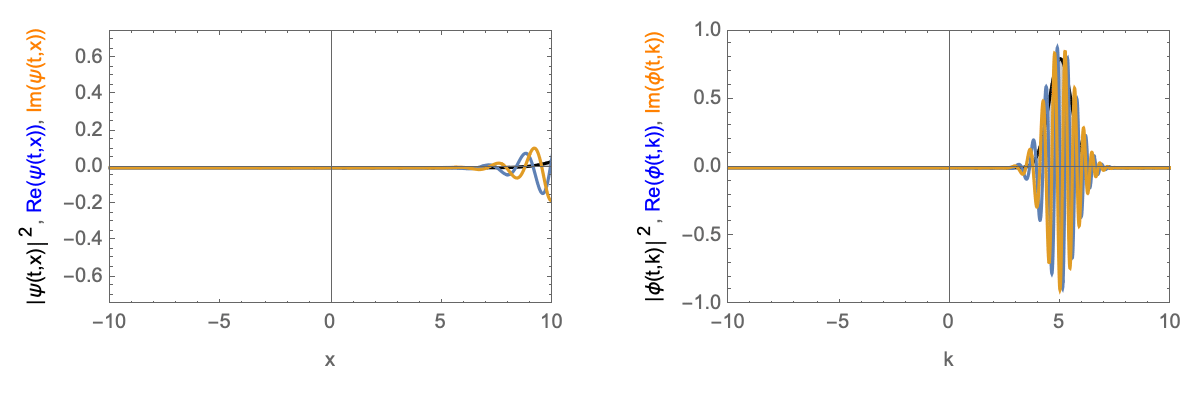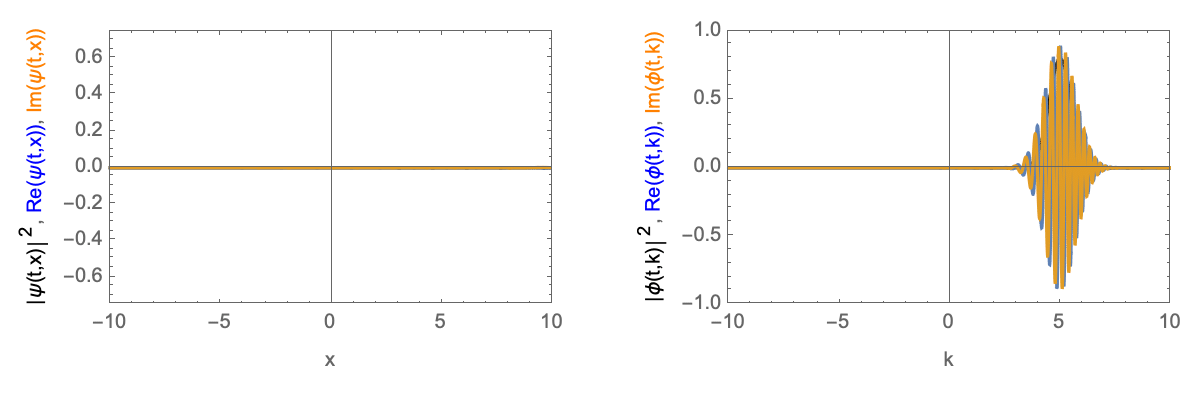Zeitentwicklung eines Gaußschen Wellenpakets mit endlicher Geschwindigkeit. Links im Realraum, rechts im Impulsraum.
Zeitentwicklung eines Gaußschen Wellenpakets mit endlicher Geschwindigkeit über eine Potentialstufe. Der potentiellen Energiestufe ist kleiner (oben) gleich (Mitte) oder größer (unten) als die kinetische Energie des Teilchens.
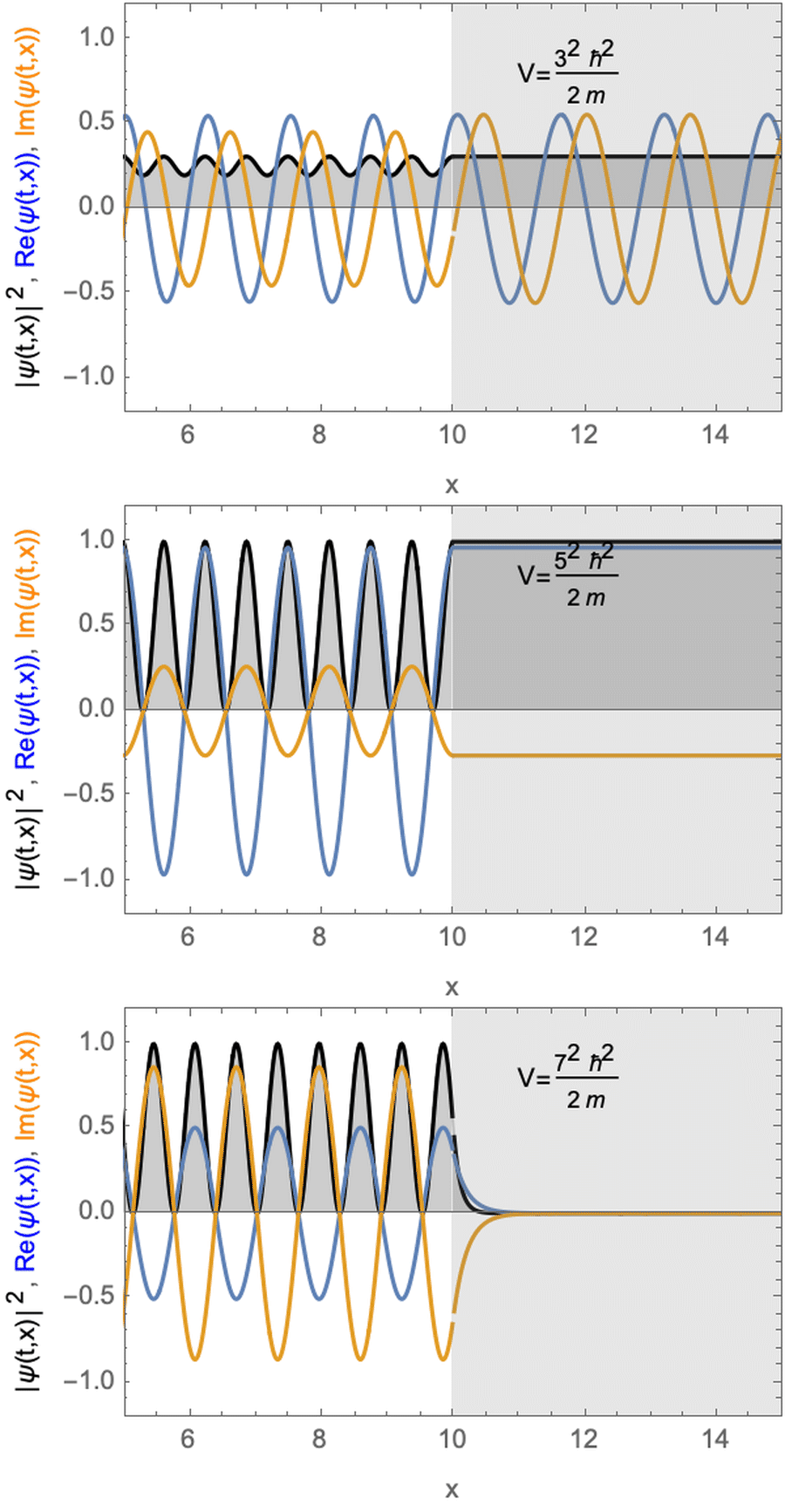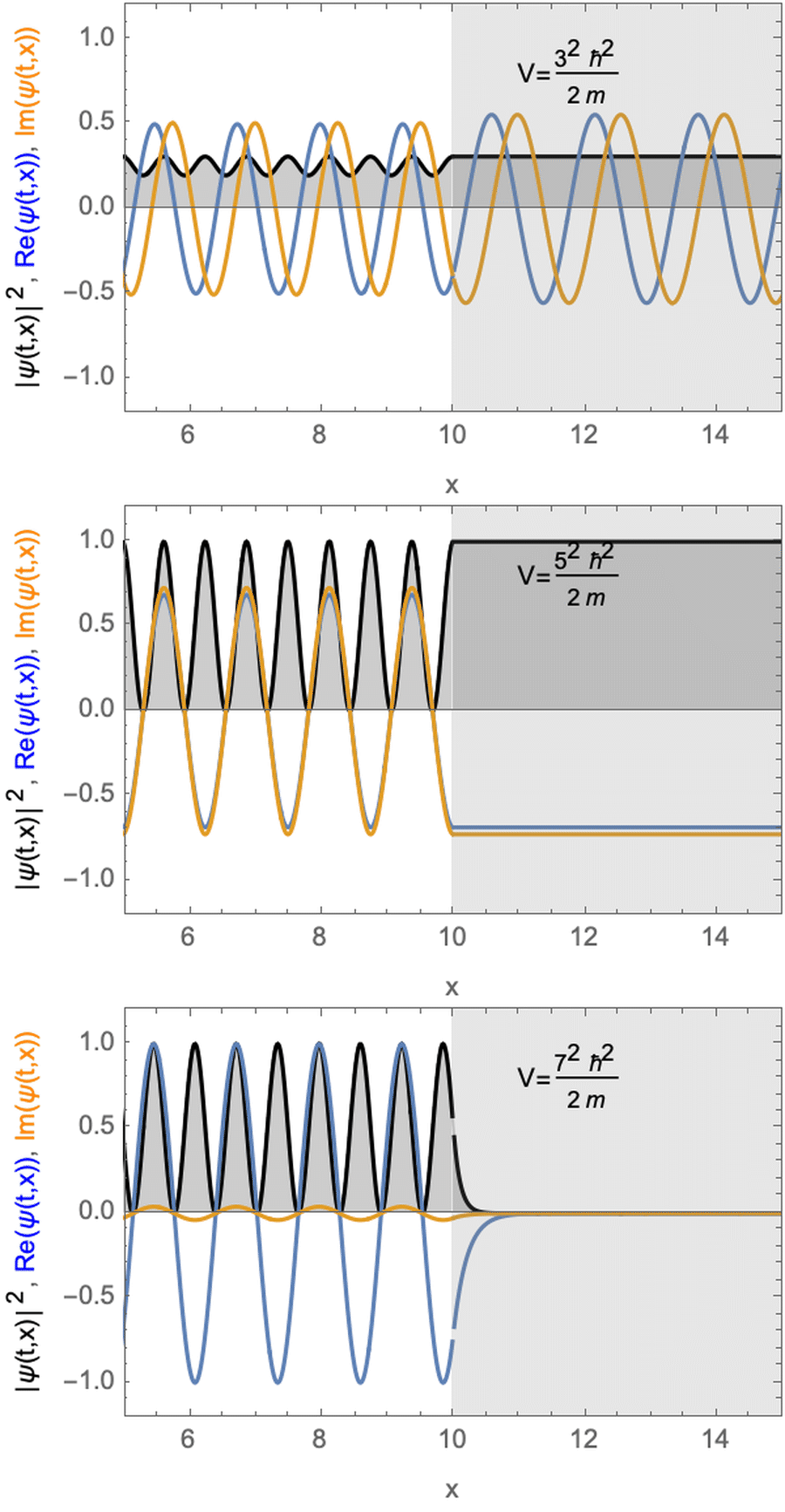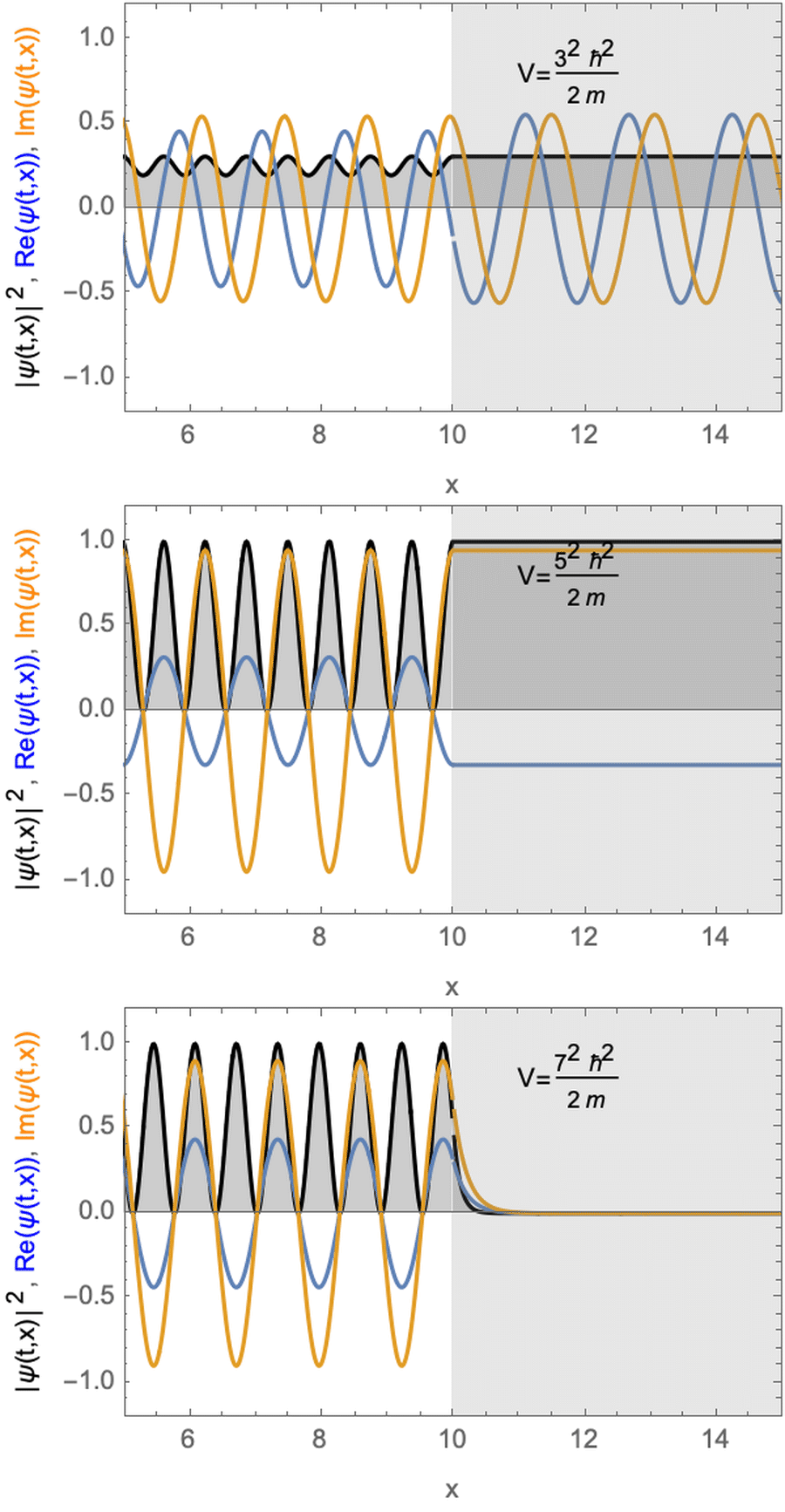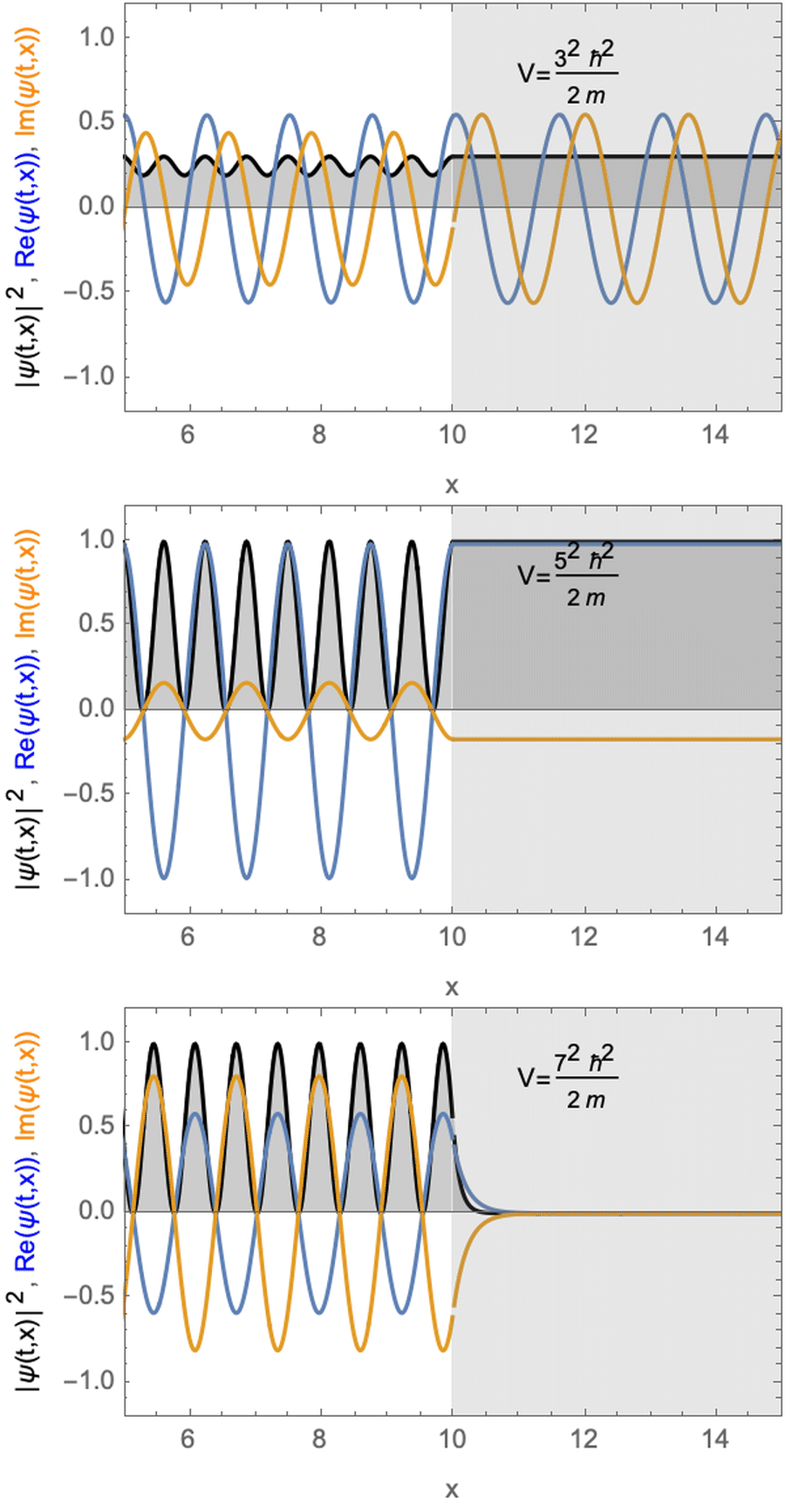Stationäre Lösung für ein Teilchen mit potentieller Stufe. Der potentiellen Energiestufe ist kleiner (oben) gleich (Mitte) oder größer (unten) als die kinetische Energie des Teilchens.
Wellenpaket, das eine Potentialbarriere passiert. Das Potential ist größer (oben) gleich (Mitte) oder kleiner (unten) als die kinetische Energie des Teilchens.
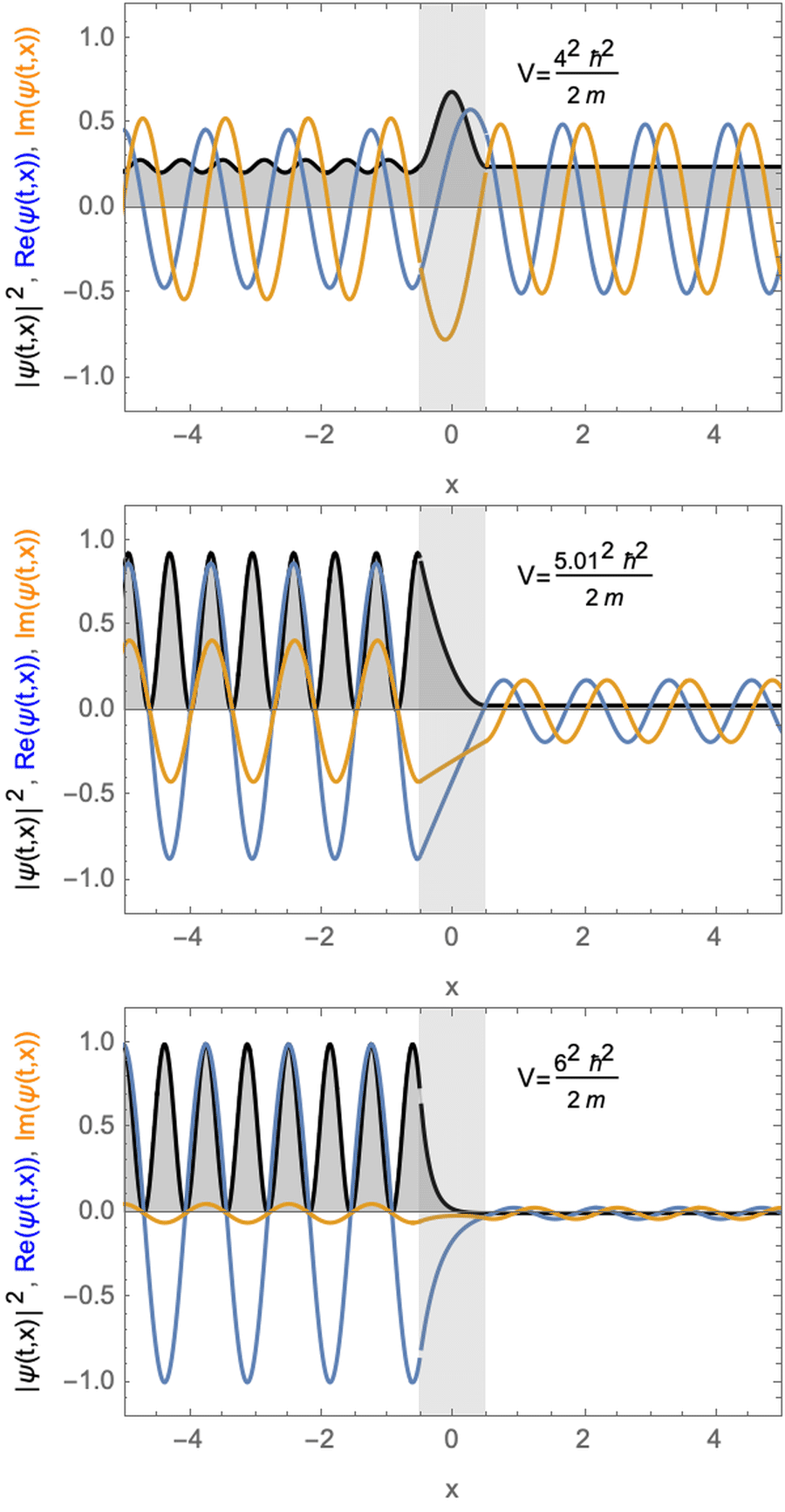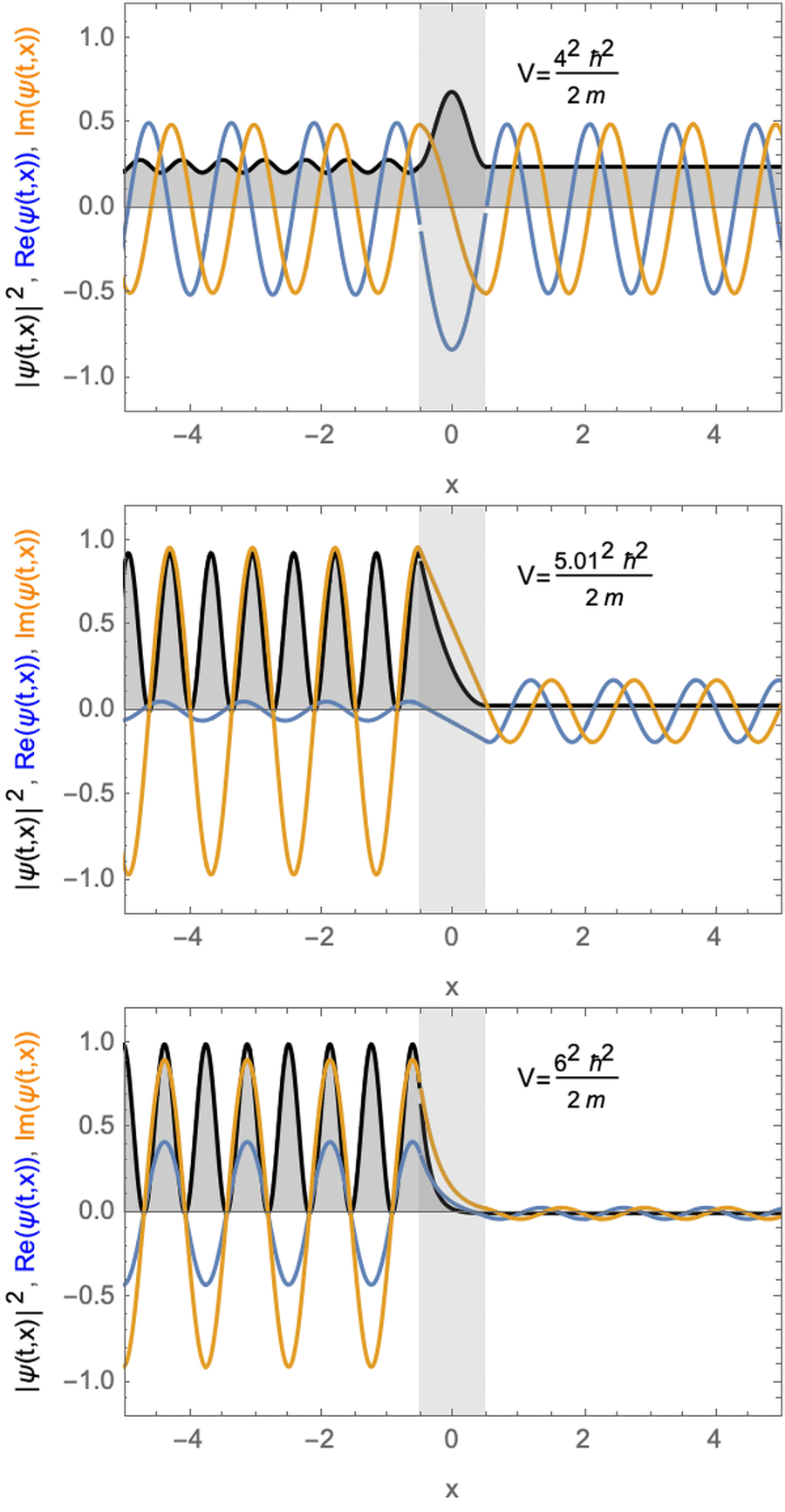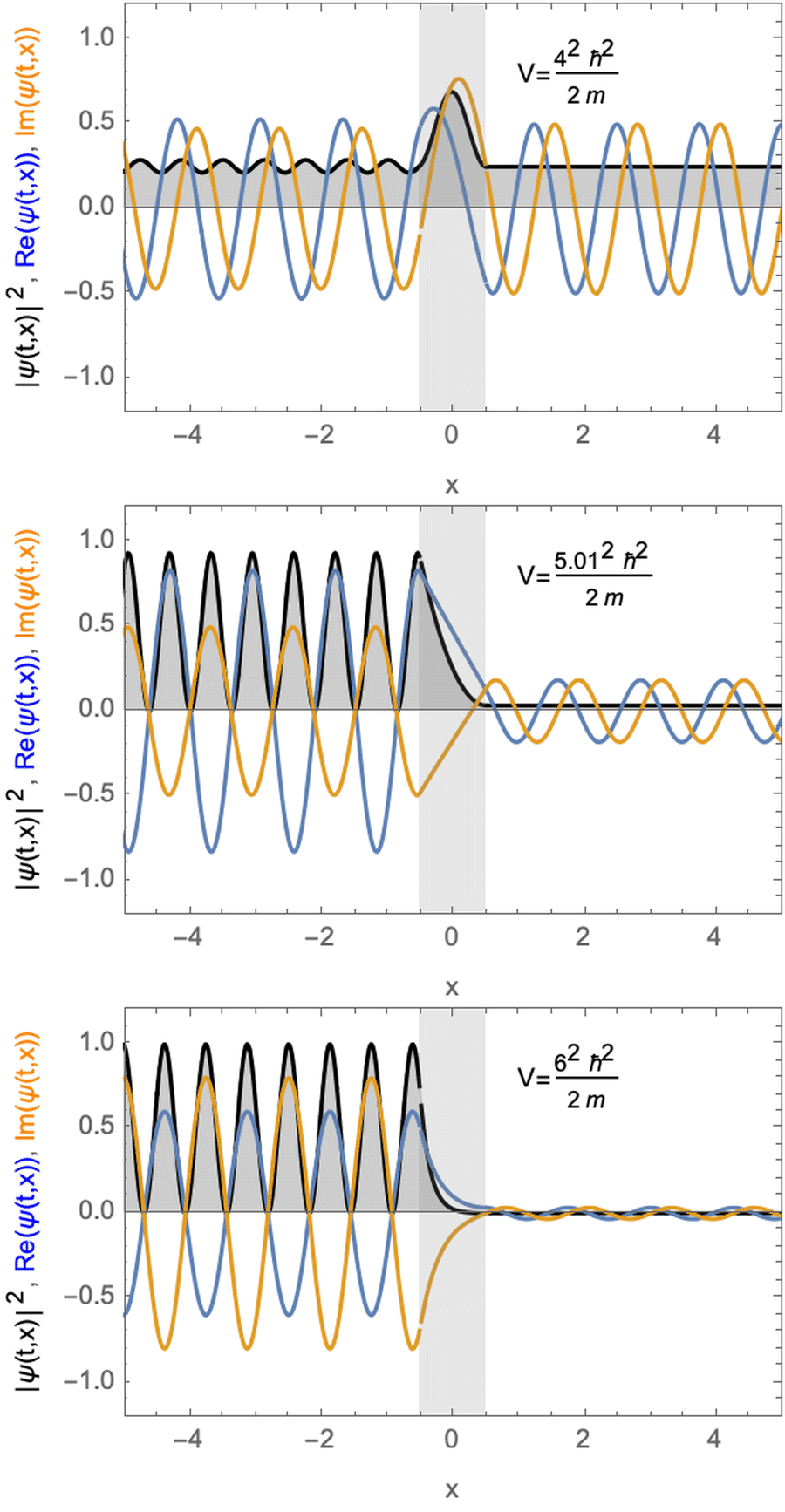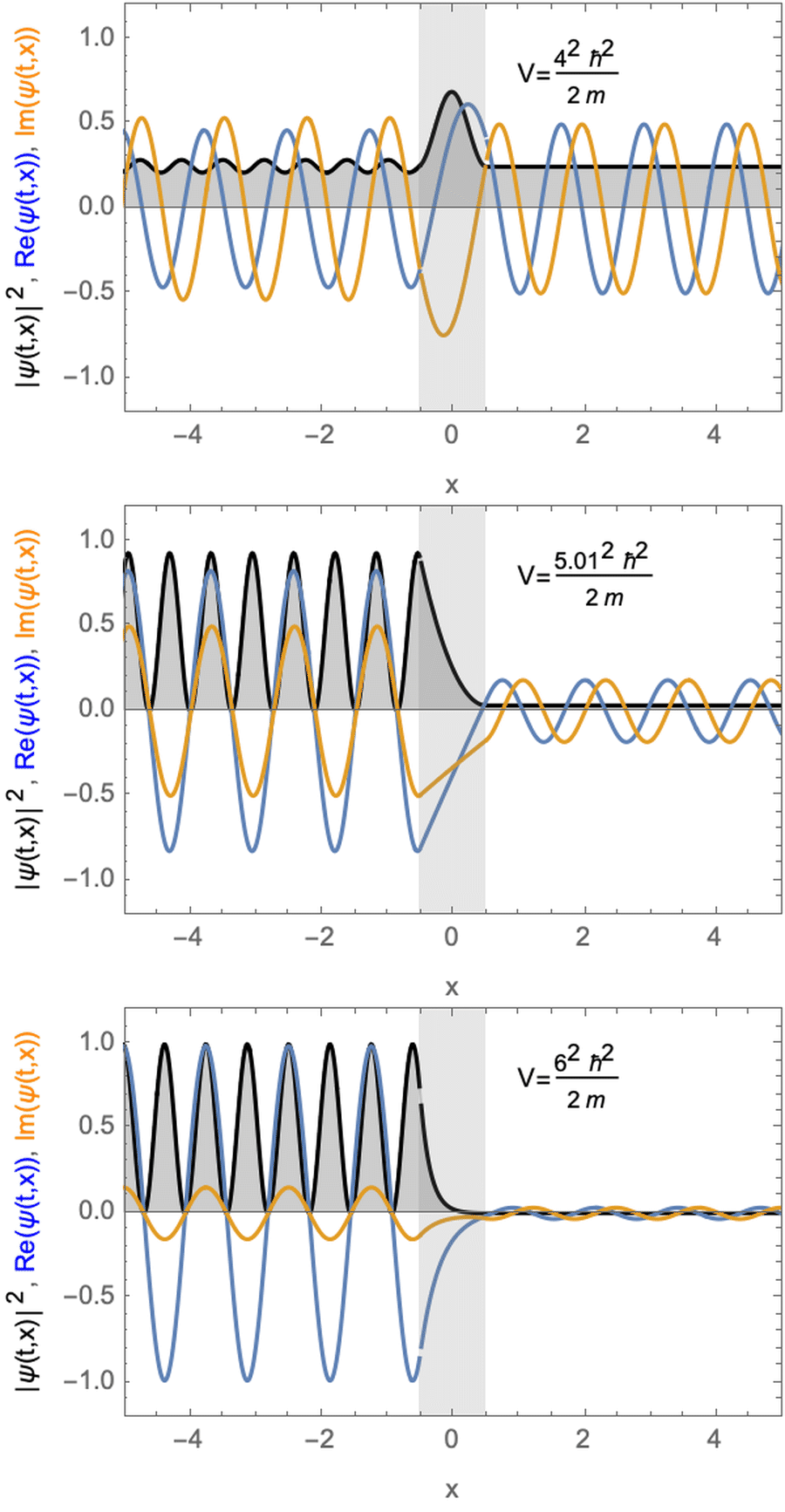Stationäre Lösungen für ein Teilchen mit Potentialbarriere. Das Potential ist größer (oben) fast gleich (Mitte) oder kleiner (unten) als die kinetische Energie des Teilchens.
Zeitliche Entwicklung eines Teilchens, dargestellt durch ein Gaußsches Wellenpaket in einem Kasten.
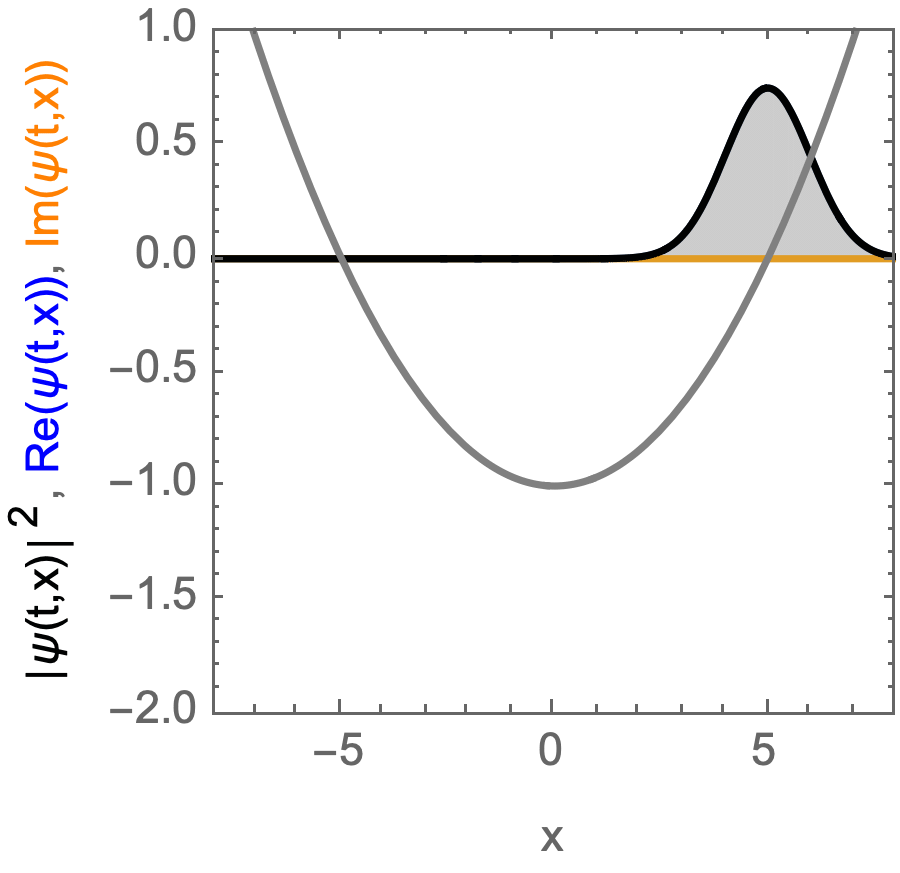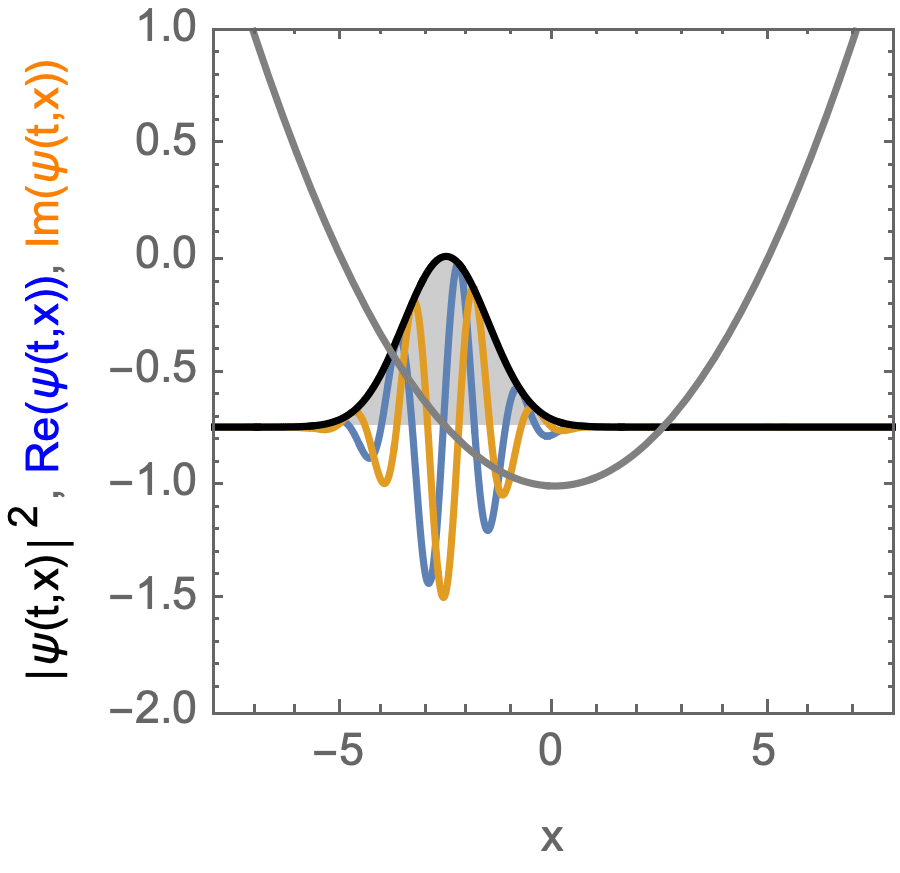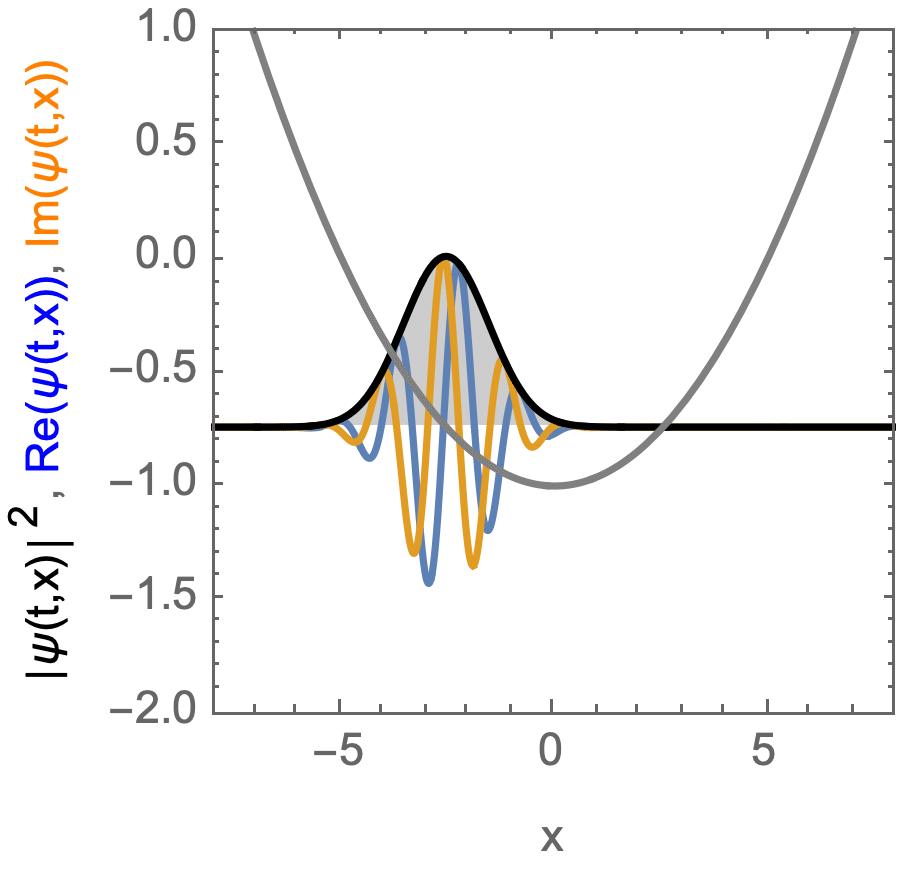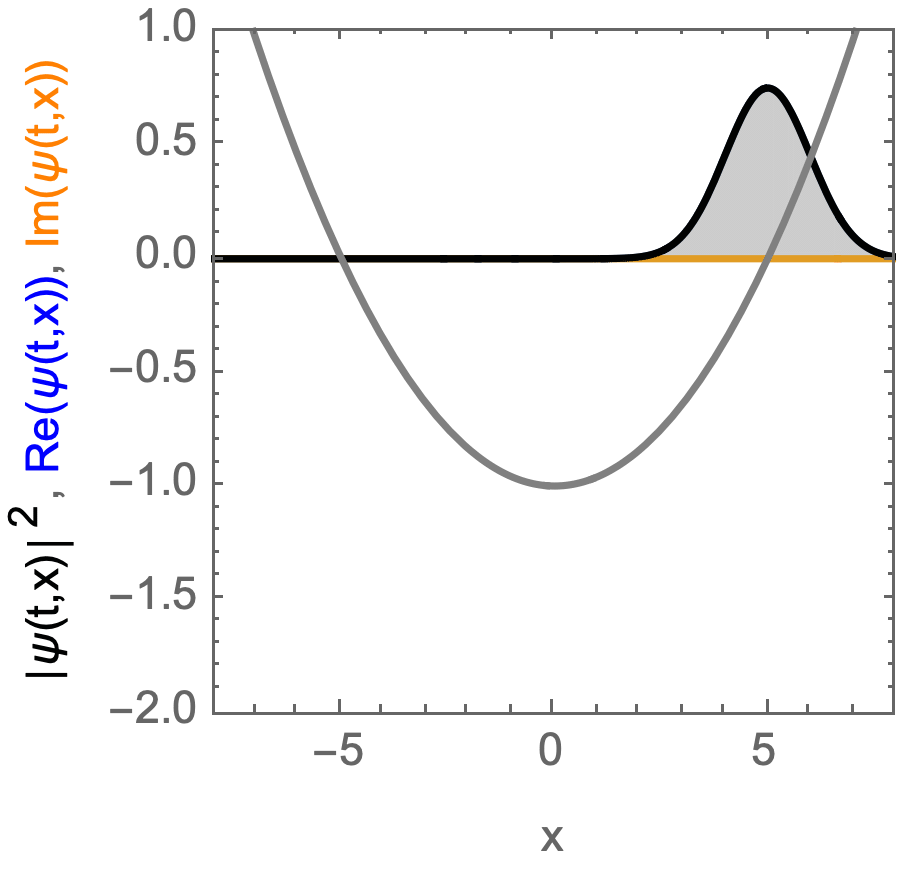Kohärenter Zustand, der sich in einem harmonischen Potential bewegt.