Department > Lectures > Summer Term 2022 > Theoretische Physik IV (Quantenmechanik)

Theoretische Physik IV (Quantenmechanik)

Lecturer: Maurits W. Haverkort

During this lecture we will follow the script written for this semester. The script is available in English and German. Chapter 11, on relativisitc effects, chapter 13 on response theory and section 9.4 as well as the second half of chapter 7 (from 7.5.8 onwards) are not part of the exam. We will spent roughly one week per chapter. We assume that the first chapters are partly repetitions of your previous PEP3 lecture. The script is relatively extensive, its lenght is a result of working out many problems in detail.

Beside the script many good textbooks on quantum mechanics are available. A few options are listed below.

The lectures are on Tuesday and Thursday from 11:15 to 13:00, starting on Thursday the 21st of April. You will recive one homework problem per week and need to return this online until Friday evening. The Homework will be discussed in the tutorials the week thereafter. The first homework is due on Friday the 29th of April.

With some delay most of the videos of the lecuteres will become available online. 

Some other textbooks:

  • S. Gasiorowicz, Quantum Physics. Wiley, 1975, 1995, 2003.
  • J. J. Sakurai, Modern Quantum Mechanics. Cambridge University Press, 1967 - 2017.
  • D. Griffiths, Introduction to Quantum Mechanics. Cambridge Univer- sity Press, 2004, 2018.
  • A. Messiah, Quantum Mechanics I+II. North-Holland Publishing Co, 1961.
  • L. D. Landau and E. M. Lifshitz, Quantum Mechanics Non-Relativistic Theory. Elsevier, 1958, 1965, 1977.

A textbook related to infinite dimensional Hilbert spaces (for those interested, not part of the lecture):

  • B.P. Rynne and M.A. Youngson, Linear Functional Analysis. Springer (2008).

Lecture content

Week 16 20 - 22 April
Chapter 1
Week 17 25 - 29 April
Chapter 2+3 
Week 18 2 - 6 May
Chapter 3+4
Week 19 9 - 13 May
Chapter 4+5
Week 20 16 - 20 May
Chapter 5+6
Week 21 23 - 27 May
No lecture and tutorials on Thursday 26th of May
Chapter 6
Week 22 30 May - 3 June
Chapter 7
Week 23 6 - 10 June
No tutorials on Monday 6th of June
Chapter 7+8
Week 24 13 - 17 June
No lecture and tutorials on Thursday 16th of June
Chapter 8
Week 25 20 - 24 June
Chapter 8+9
Week 26 27 June - 1 July
Chapter 9+10
Week 27 4 July - 8 July
Chapter 12
Week 28 11 - 15 July
Chapter 11 (briefly) + 12
Week 29 18 - 22 July
Time to study.
Meeting on Tuesday 19th for questions
Week 30 25 - 29 July
Exam on Monday the 25th of July 14:15 - 17:00
Week 31 1 - 5 August
Discussion and questions of exam results

Material

Mathematica licenses are avialable here. 

Practice groups

  • Group 01 (Nils Winkler)
    17 participants
    INF 227 / SR 2.404, Mon 14:15 - 16:00
  • Group 02 (Jannik Fehre)
    15 participants
    INF 227 / SR 3.403, Mon 14:15 - 16:00
  • Group 03 (Philipp Joschko)
    19 participants
    Philos.-weg 12 / R 058, Mon 14:15 - 16:00
  • Group 04 (Andreas Kirchner)
    15 participants
    Philos.-weg 12 / R 060, Mon 14:15 - 16:00
  • Group 05 (Michael Heinrich)
    18 participants
    Philos.-weg 12 / R 070, Mon 14:15 - 16:00
  • Group 06 (Louis Jussios)
    19 participants
    Philos.-weg 12 / R 056, Tue 9:15 - 11:00
  • Group 07 (Lennart Kai Röver)
    20 participants
    Philos.-weg 12 / R 068, Tue 9:15 - 11:00
  • Group 08 (Tim Leibbrandt)
    18 participants
    Philos.-weg 12 / R 058, Tue 9:15 - 11:00
  • Group 09 (Tim Luca Ebert)
    20 participants
    INF 227 / SR 3.404, Tue 9:15 - 11:00
  • Group 10 (Maximilian Müllenbach)
    21 participants
    INF 227 / SR 2.403, Tue 14:15 - 16:00
  • Group 11 (Alena Braendle)
    17 participants
    Philos.-weg 12 / R 216, Tue 14:15 - 16:00
  • Group 12 (Heyen, Lars Helge)
    20 participants
    Philos.-weg 12 / R 056, Tue 14:15 - 16:00
  • Group 13 (Christoph Smaczny)
    18 participants
    INF 227 / SR 1.403, Tue 14:15 - 16:00
  • Group 14 (Natalia Oreshkina)
    englisch
    15 participants
    Philos.-weg 12 / R 059, Tue 14:15 - 16:00
  • Group 15 (Mathias Backes)
    19 participants
    INF 227 / HS 2, Tue 16:15 - 18:00
  • Group 16 (Zoltan Harman)
    19 participants
    INF 227 / SR 2.402, Wed 14:15 - 16:00
  • Group 17 (Cedric Quint)
    18 participants
    Philos.-weg 12 / R 058, Wed 14:15 - 16:00
  • Group 18 (Yannic Pietschke)
    24 participants
    Philos.-weg 12 / kHS, Wed 16:15 - 18:00
up
Theoretische Physik IV (Quantenmechanik)
summer term 2022
Haverkort
Link zum LSF
ss22-ptp4
332 participants
The first lecture will be on Thursday the 21st of April at INF227 HS1. We will stream our lectures via Zoom, but advise you to be present in real life.
The exam will be on Monday the 25th of July from 14:15 - 17:00. 
Thomson scattering of electromagnetic radiation from a hydrogen atom
Compton scattering of electromagnetic radiation from a hydrogen atom
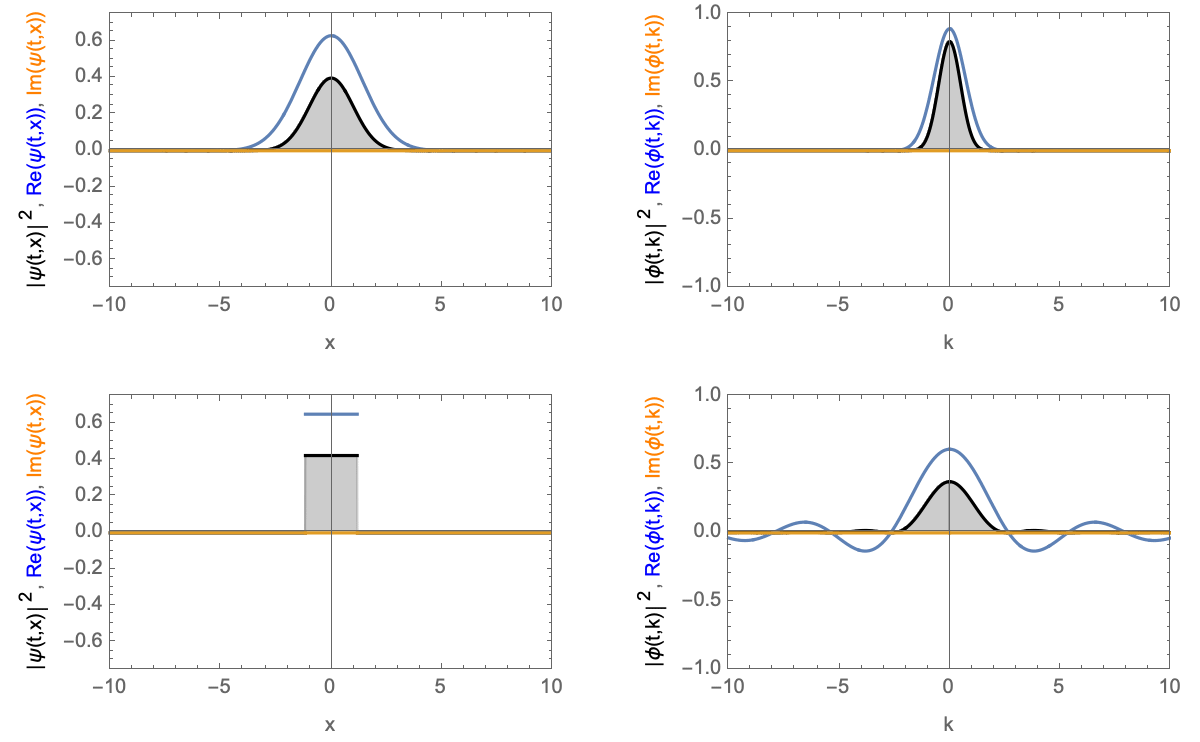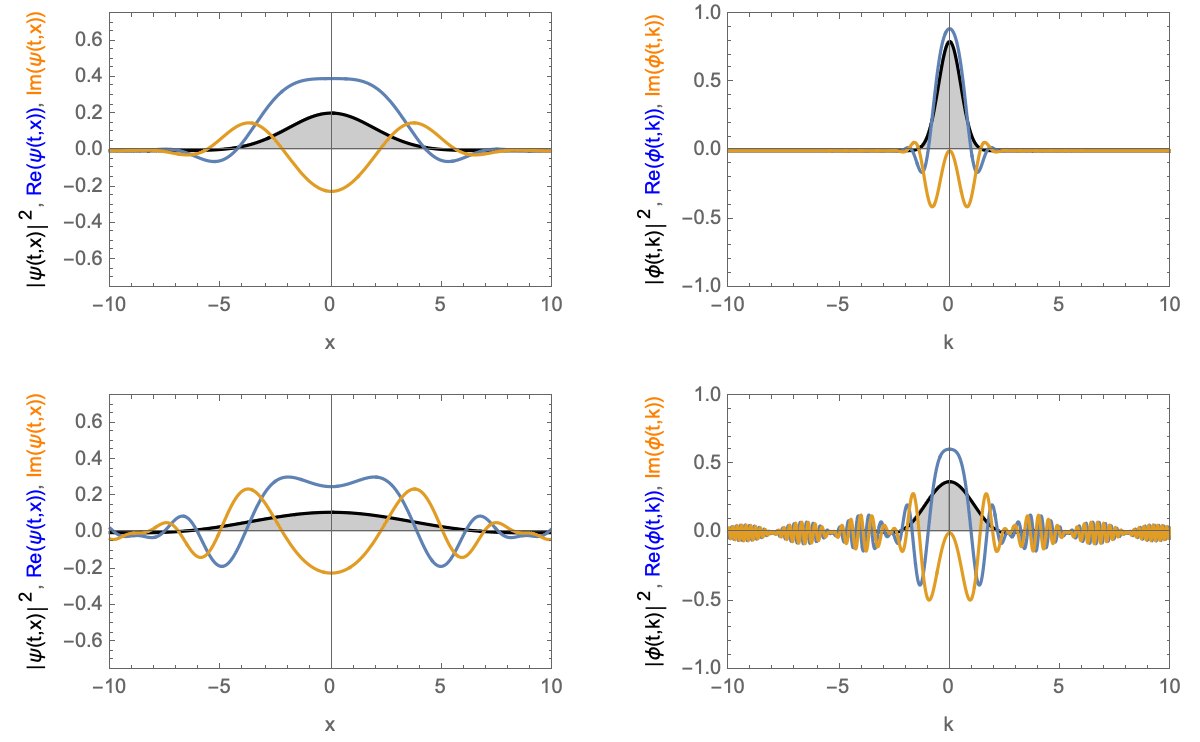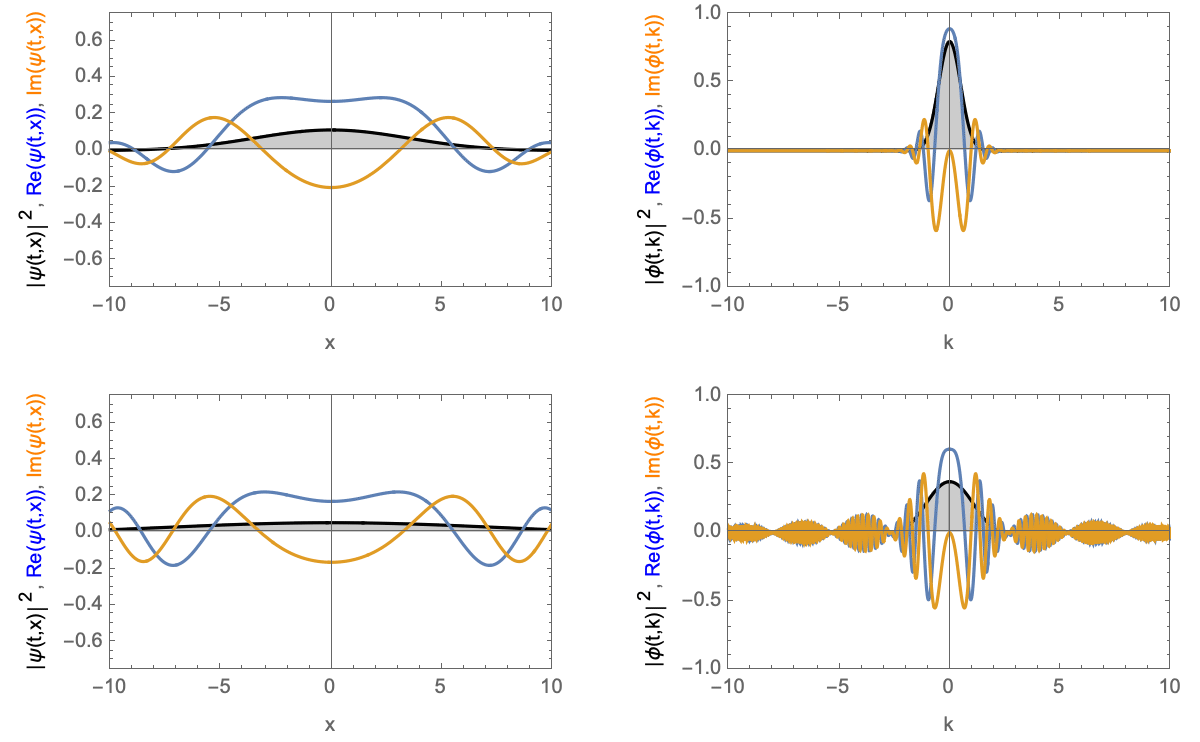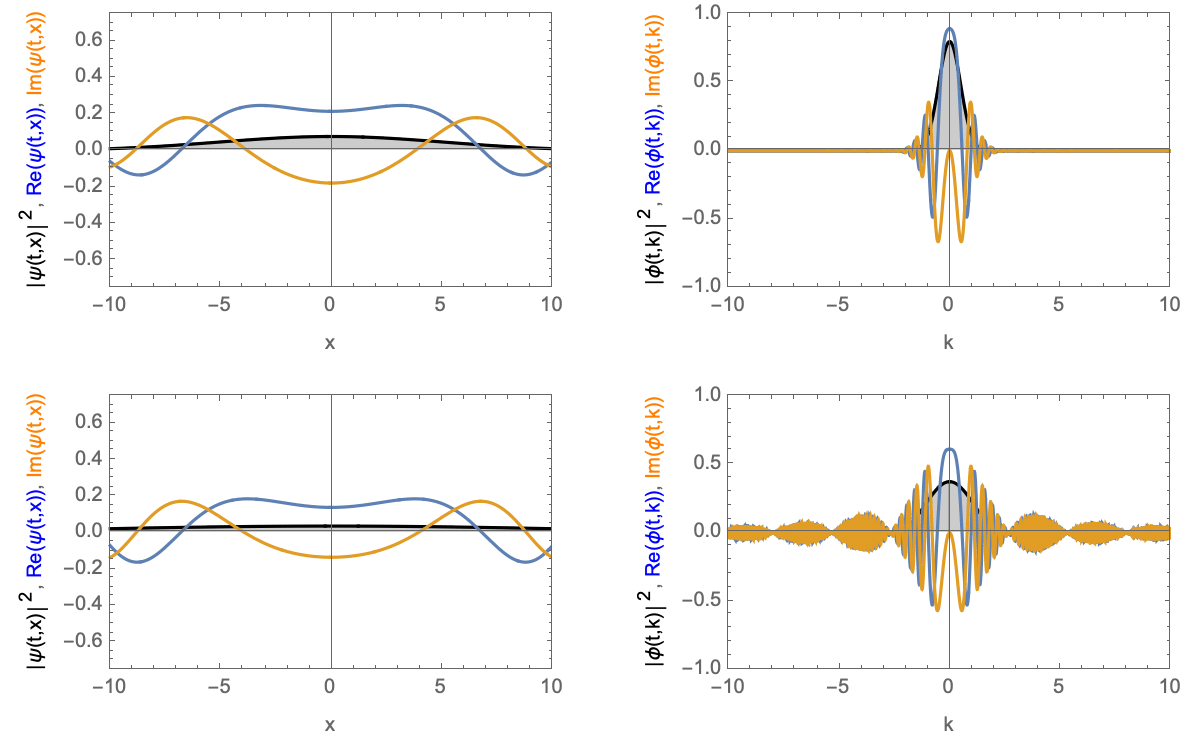Time-evolution of a wave-packet with zero velocity. Top Gaussian wave-packet, bottom block wave-packet. Left in real-space, right in momentum-space.
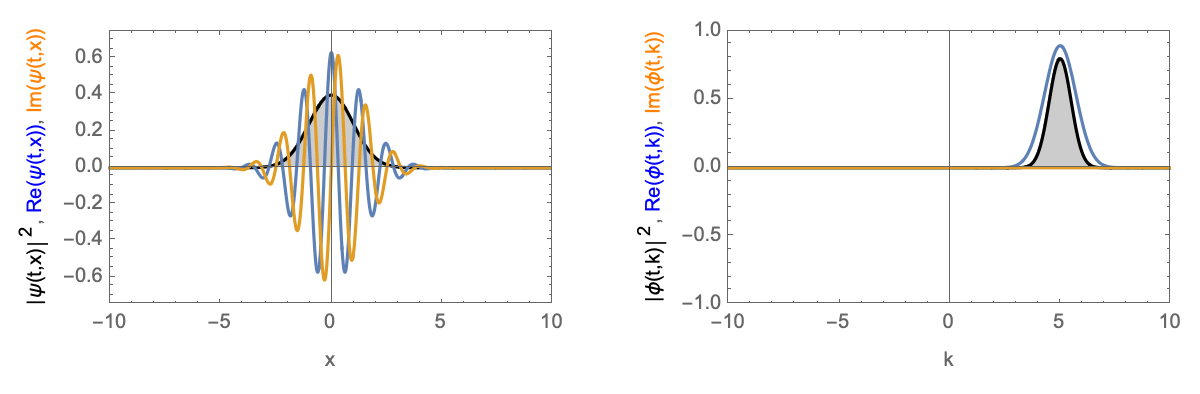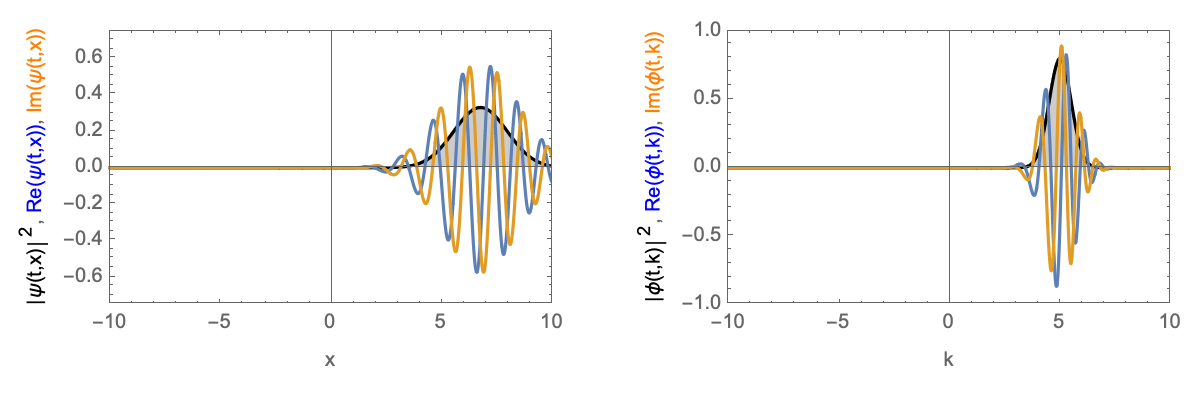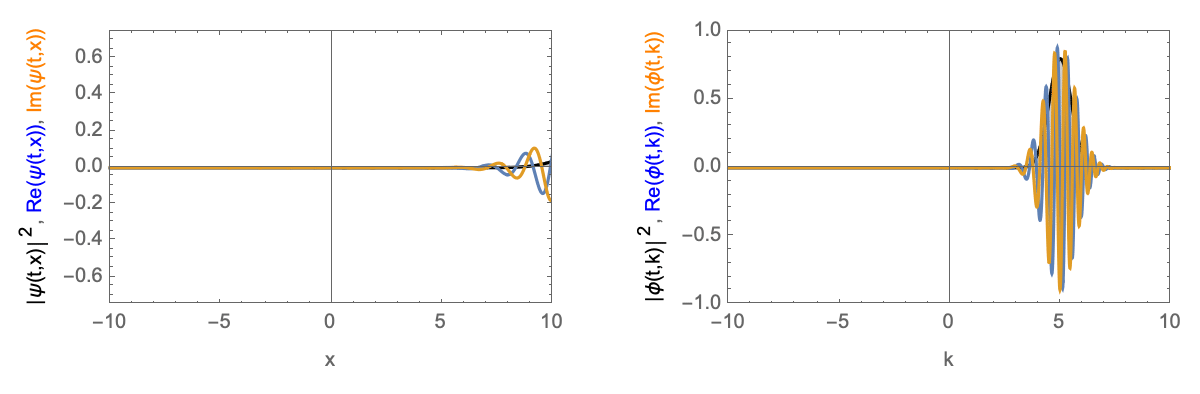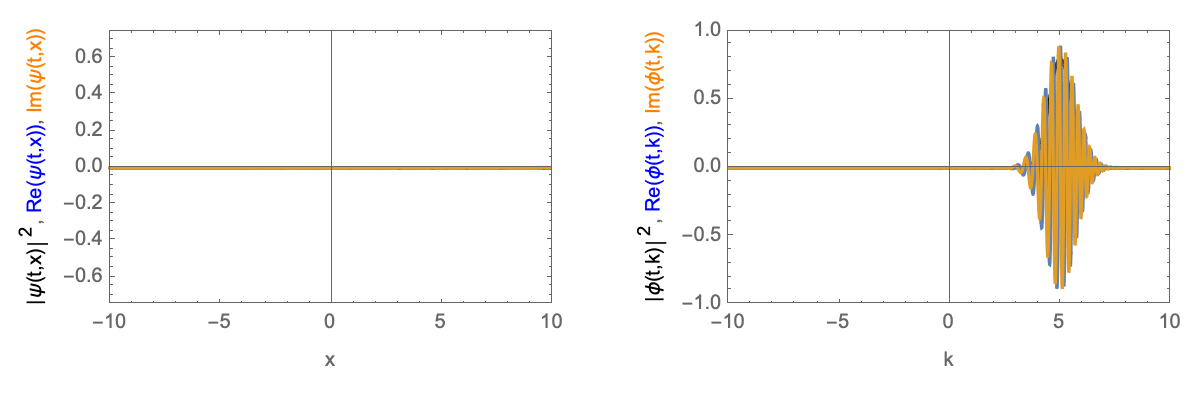Time-evolution of a Gaussian wave-packet with finite velocity. Left in real-space, right in momentum-space.
Time-evolution of a Gaussian wave-packet with finite velocity across a potential step. The potential energy step is smaller (top) equal (middle) or larger (bottom) than the kinetic energy of the particle.
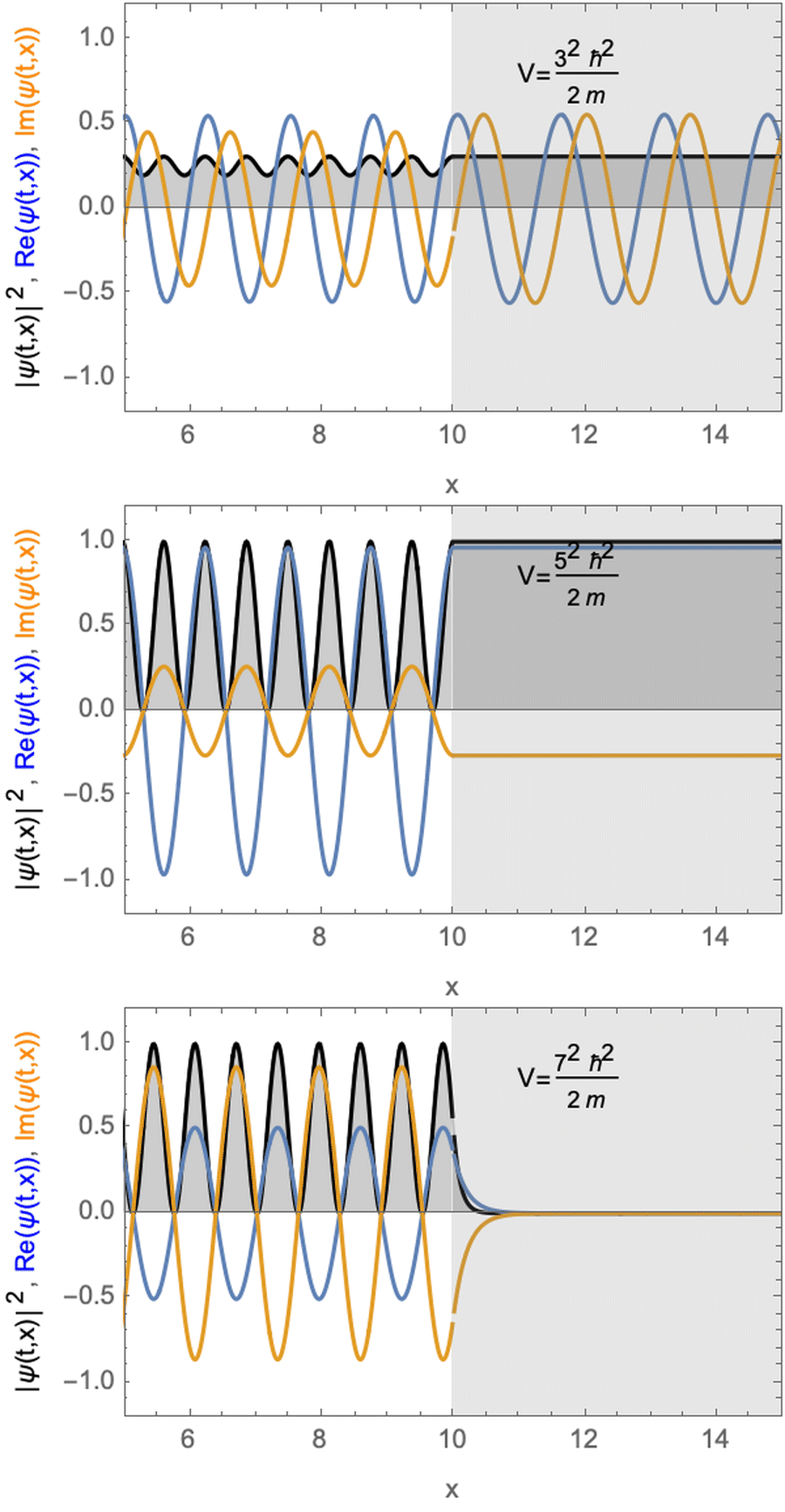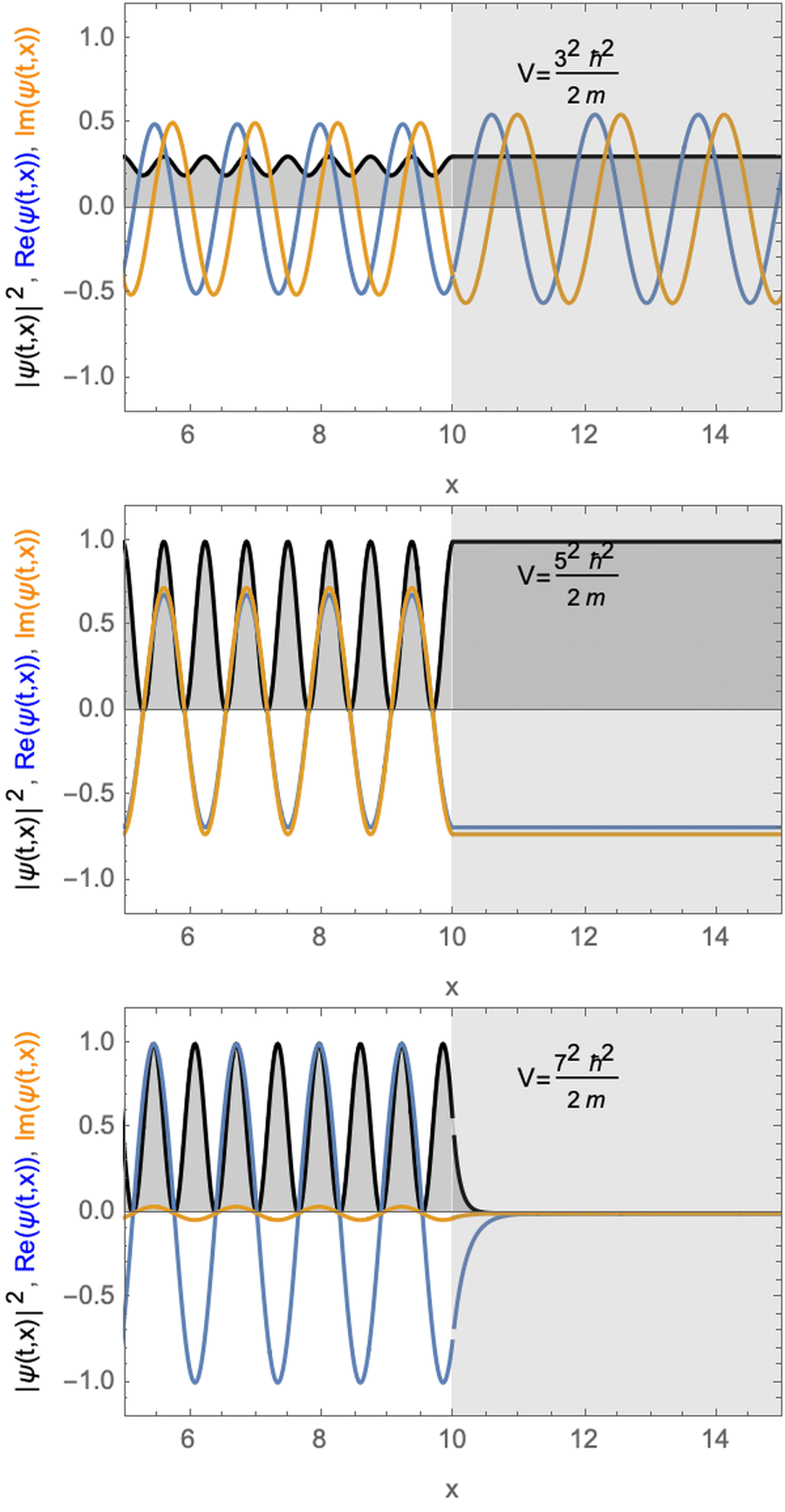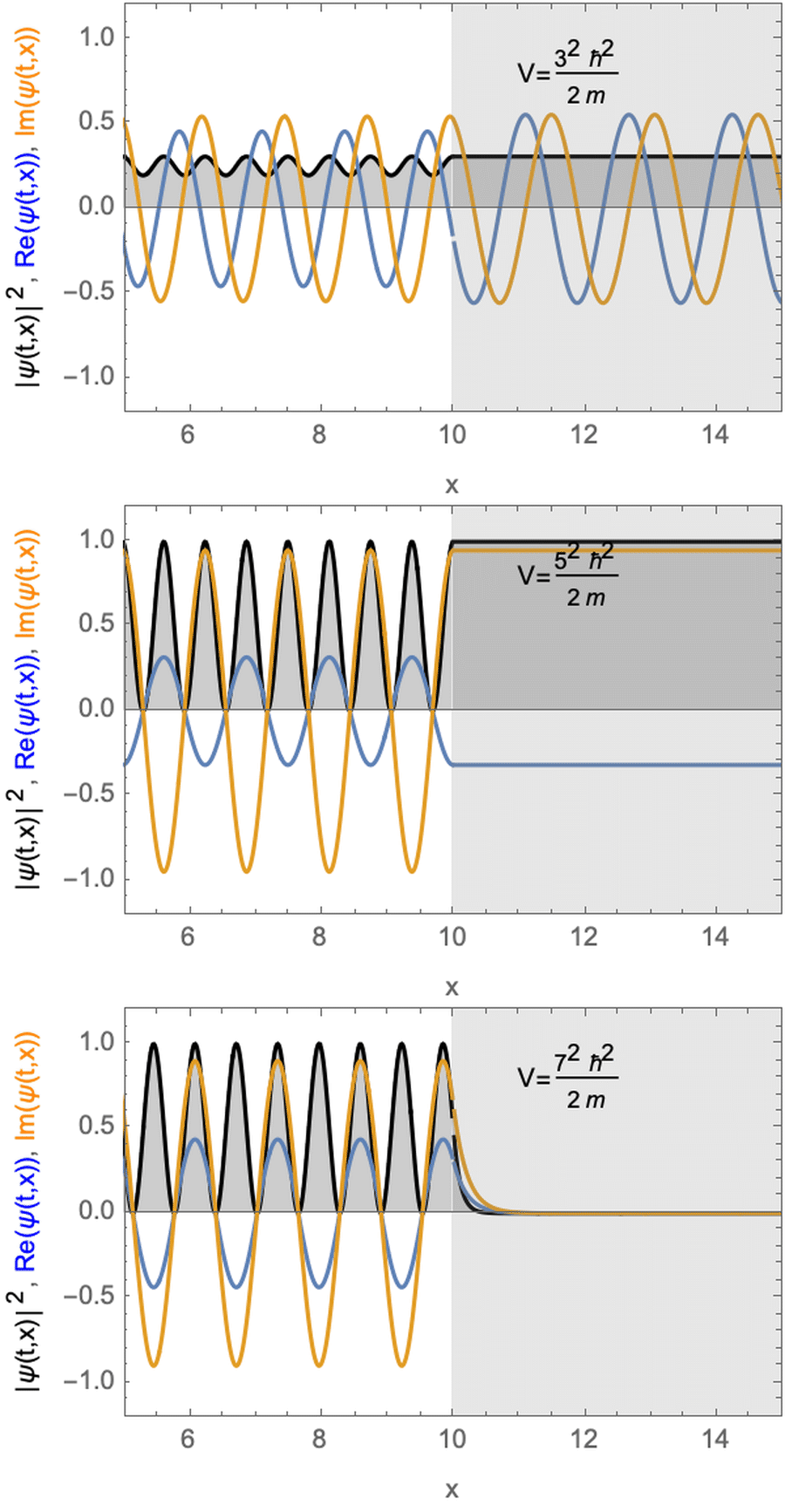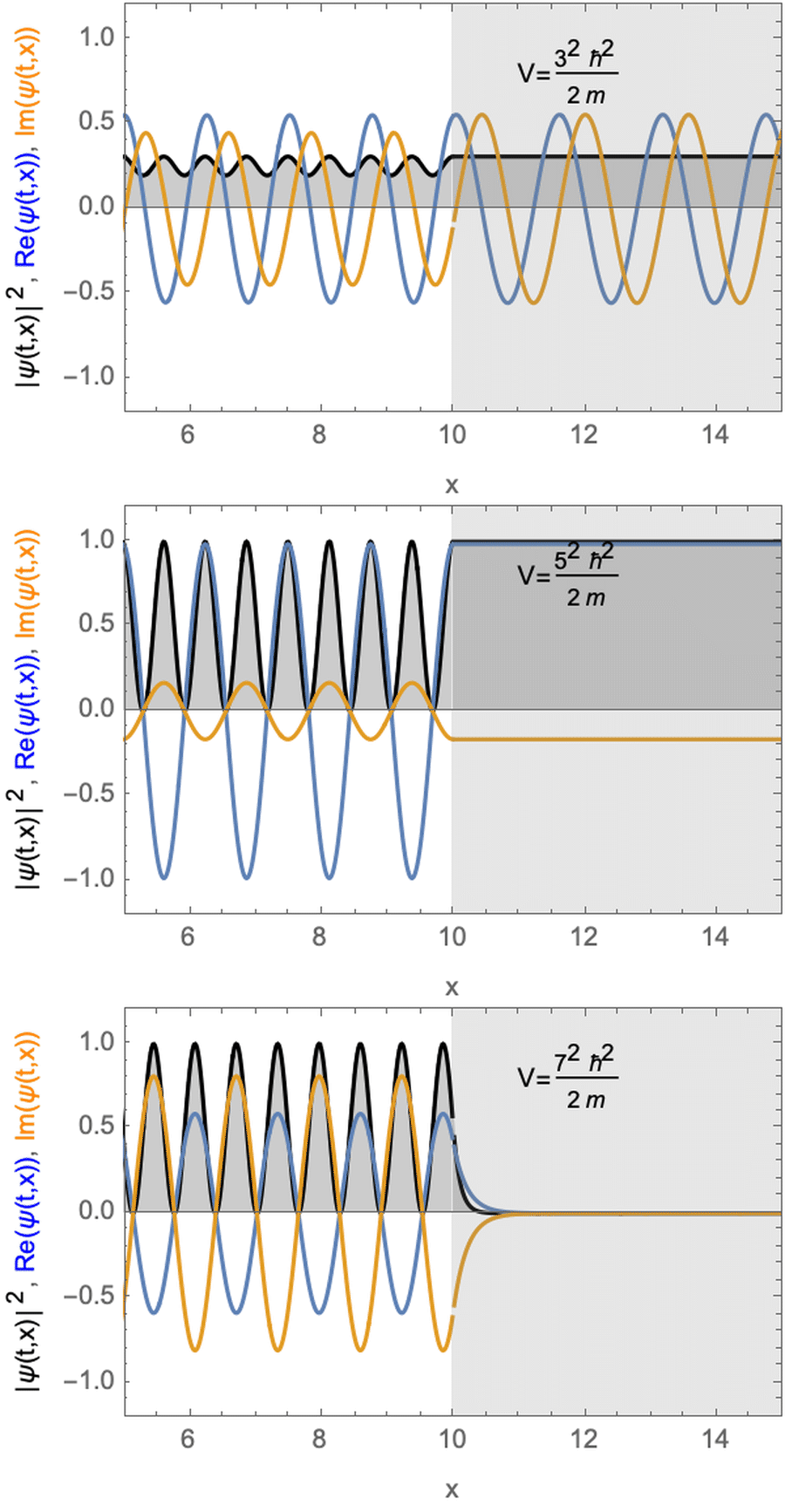Stationary solution for a particle with a potential step. The potential energy step is smaller (top) equal (middle) or larger (bottom) than the kinetic energy of the particle.
Wave-packet traveling past a potential barrier. The potential is larger (top) equal (middle) or smaller (bottom) than the kinetic energy of the particle.
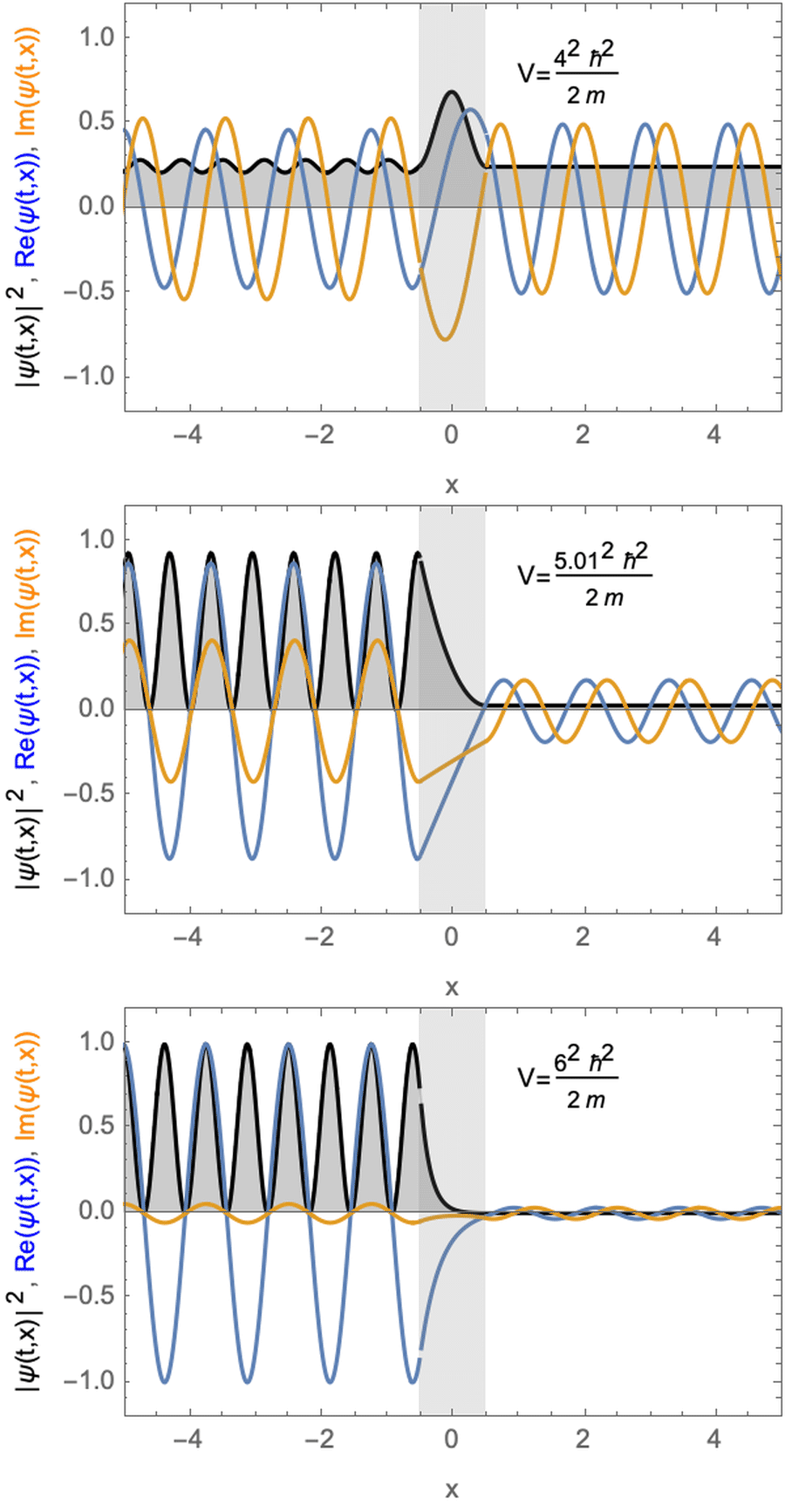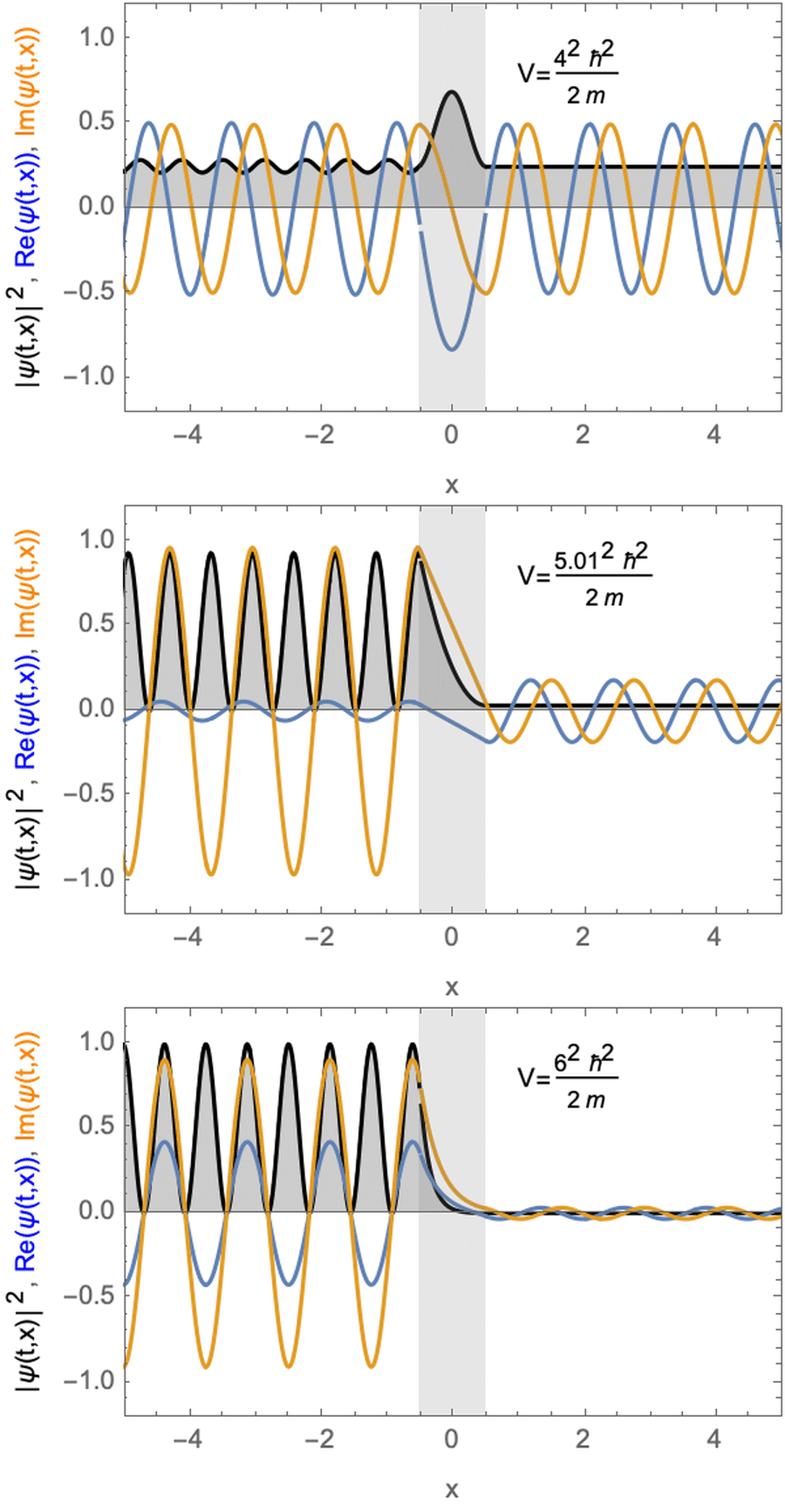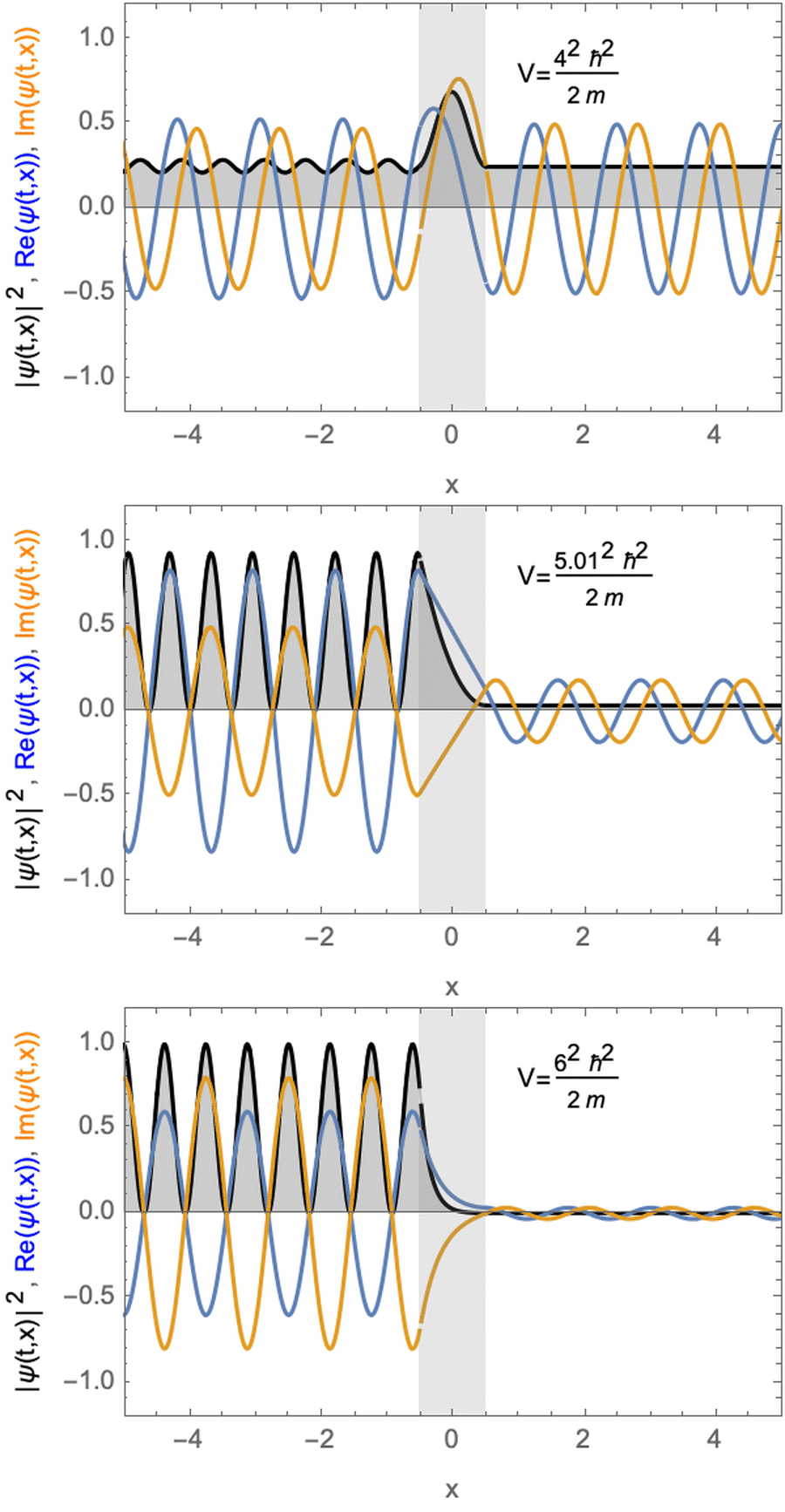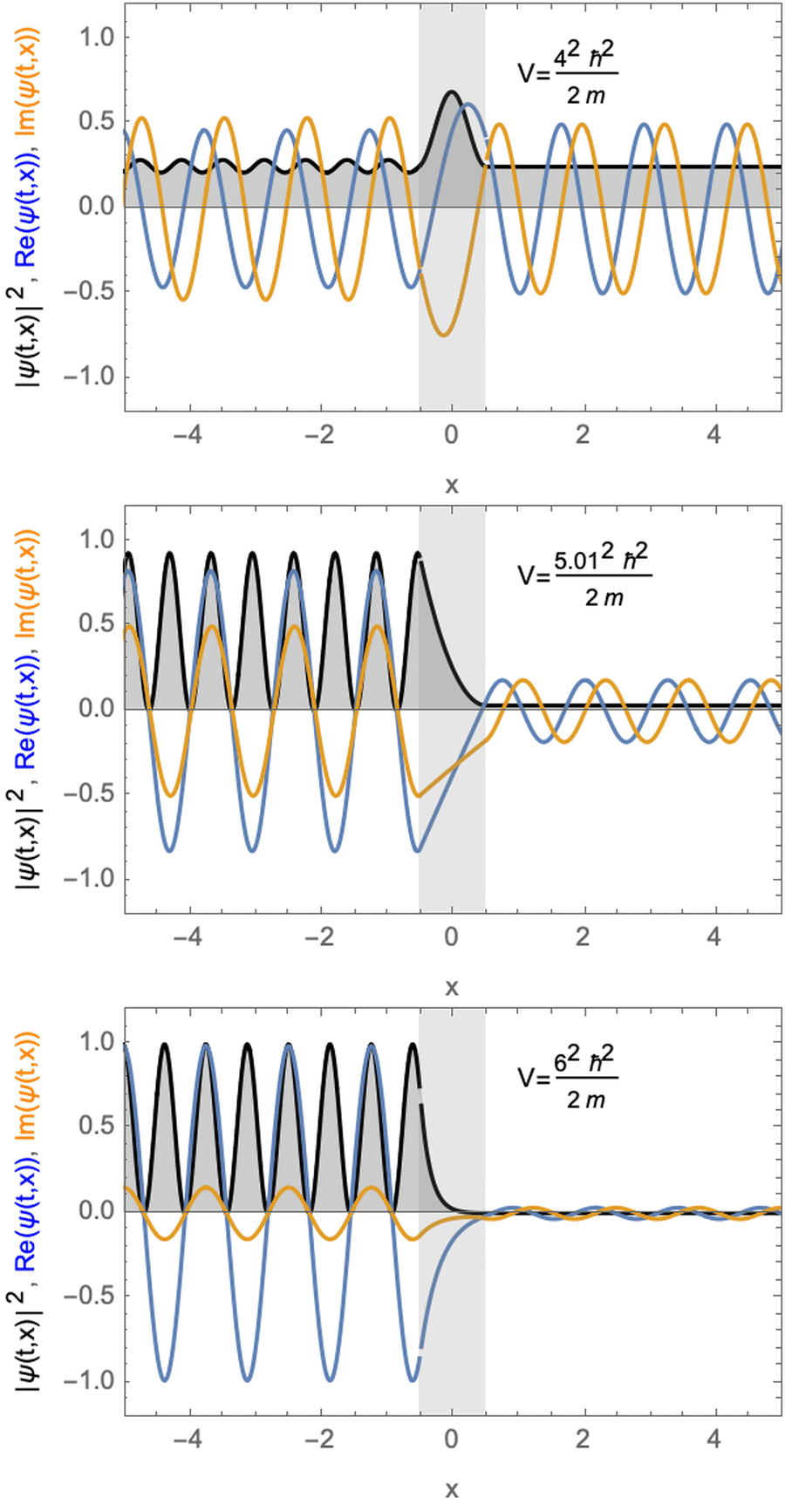Stationary solutions for a particle with a potential barrier. The potential is larger (top) almost equal (middle) or smaller (bottom) than the kinetic energy of the particle.
Time evolution of particle represented by a Gaussian wave packet in a box.
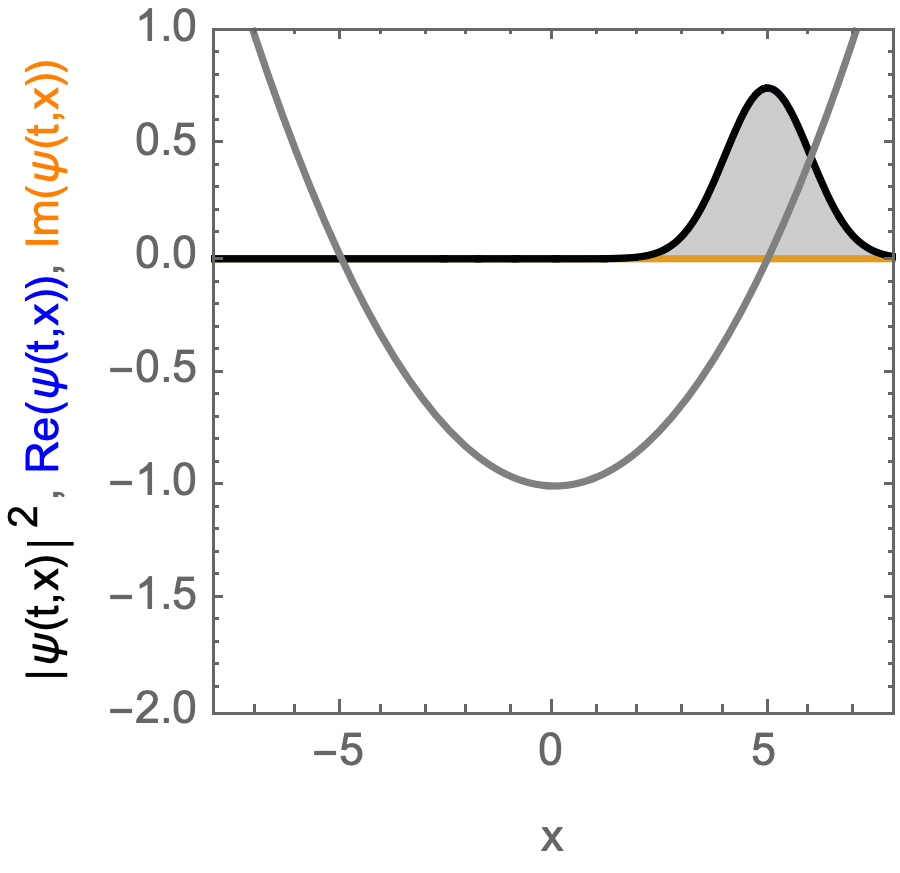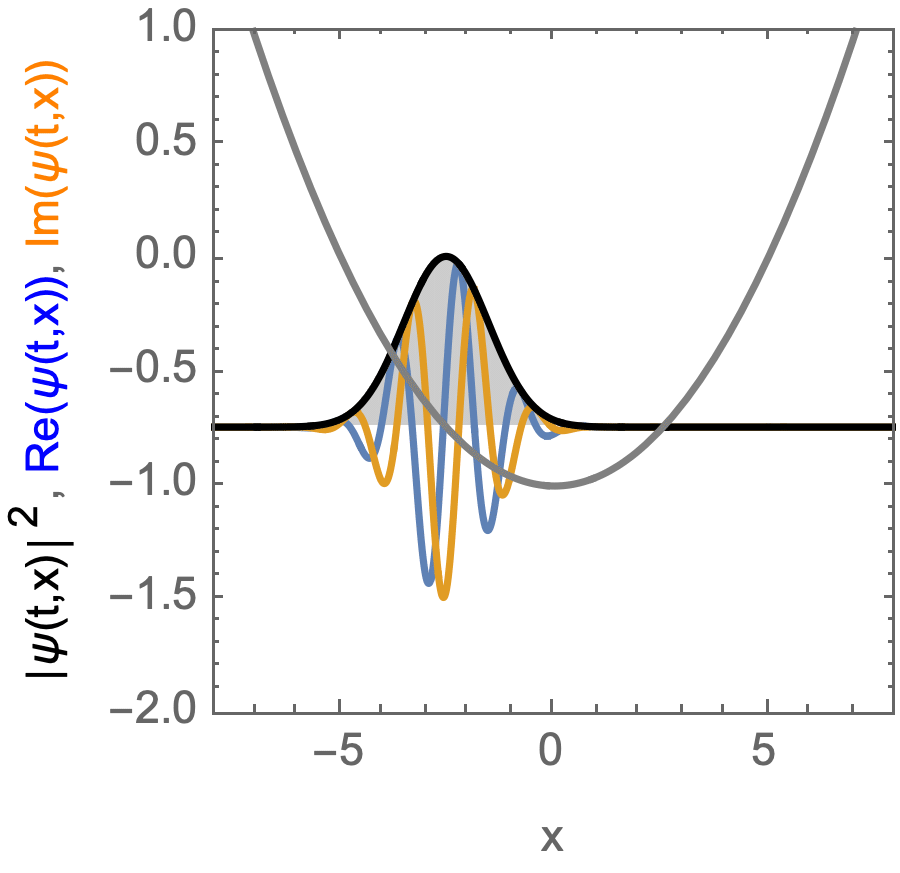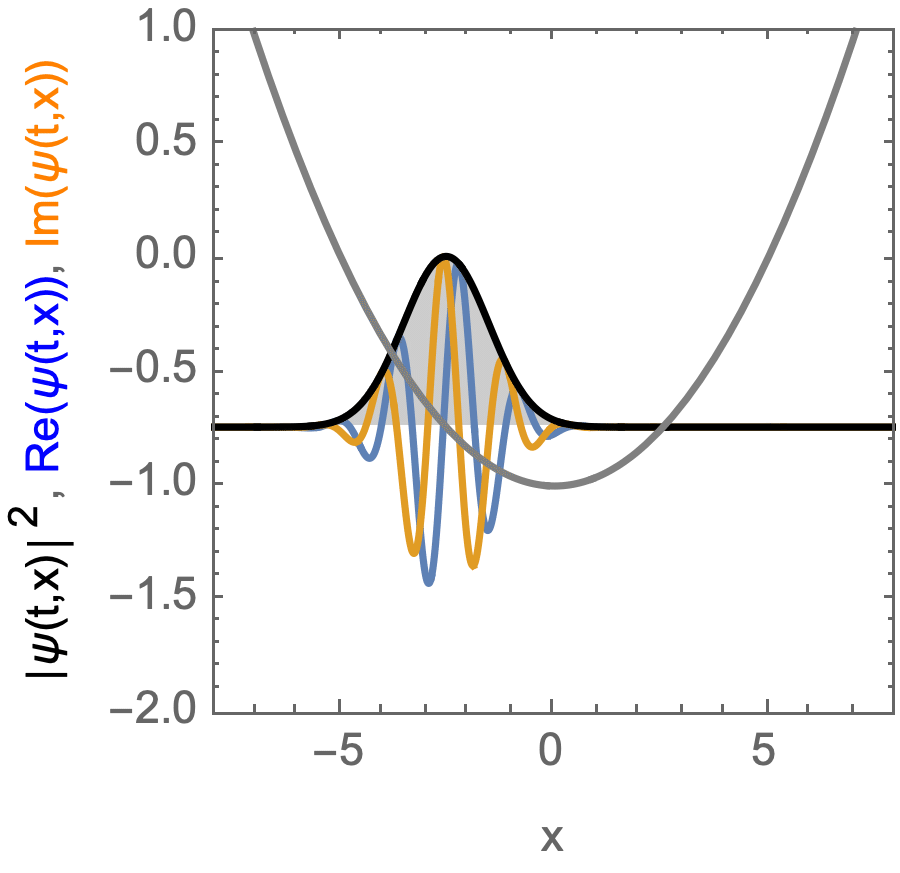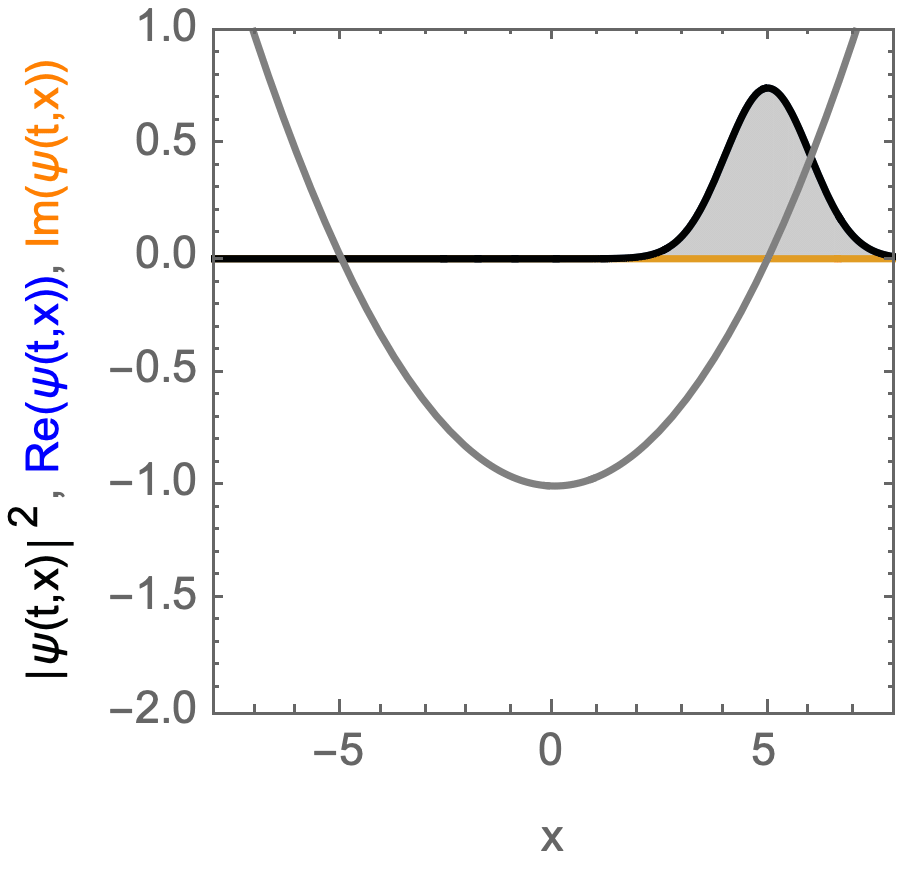Coherent state, moving in an Harmonic potential.