General Relativity
Welcome

Lecturer:
Priv.-Doz. Dr. Matteo Maturi (ITA/ZAH, ITP)
Head tutor: Nadine Nußbaumer (nussbaumer_n@thphys.uni-heidelberg.de)
Space and time:
- Summer semester, 2023
- From April 17th to July 19th
- Monday 09:15-11:00 (INF308/HS 2)
- Wednesday 09:15-11:00 (INF308/HS 2)
Overview:
Gravity is the weakest of all forces in nature and yet it shapes our universe on all scales, from humans bind to Hearth up to defining the dynamics of the entire universe. The lectures will open the path in the understanding on gravity as described by the theory of General Relativity. The students will learn about the properties of flat and curved space-times, the behaviour of massive and massless particles in presence of gravity, black holes a different kinds, gravitational waves, the dynamic of the universe, etc...
Prerequisites:
PTP2, PTP3 is helpful but not mandatory.
Format:
The lectures will be held in person and will be recorded. Lecture notes about what will be present at the blackboard and additional material will be provided. The notes will be complementary to other material/books and present full derivations. I will start slow to build a solid background. The lectures and exercise classes are held in English and will be recorded.
Enrollment:
To get credit points for the lectures it is necessary to enroll through this website.
If you are still missing the credentials (immatriculation, ID number, ...) and can not log-in, ask the head tutor to be enroll manually.
Material and exercises:
You find everything in this page.
Question session:
Wednesday, July 26th, 2023, from 3pm to 5pm; room R 068, Philosophenweg 12
Exam:
Written. Thursday, July 27th, 2023 from 2pm to 5pm; Lecture halls INF 227 HS1 and HS2
Exam review:
Tuesday, August 1st, 2023, from 2pm to 4pm; Lecture hall nHS, Philosophenweg 12
Retake exam:
Written. Wednesday, October 11th, 2023 from 2pm to 5pm; Lecture halls gHS, Philosophenweg 12
Retake exam review:
Friday, October 13th, from 2pm to 4pm; Seminar room (SR) on the 3rd floor, Philosophenweg 12
Admission to the exam:
Attend at least 50% of the tutorials AND gain 3 points by: Presenting an exercise (1 point) or actively participating in the discussion during the tutorials (max 1 point per tutorial). If < 3 points are acquired, it is required to hand in 3 full exercise sheets that will be graded.
Lehre, Studium und Forschung:
Lecture Token MKTP3.1 (8CP): LSF
First Ever ray tracing simulation of a black hole (1979 © Jean-Pierre Luminet/CNRS Phototheque). This is the computer used to realize it: IBM7040. At the time programs was loaded on the computer with a punch card.

First ever 'picture' of a shadow of a black hole (EHT collaboration)

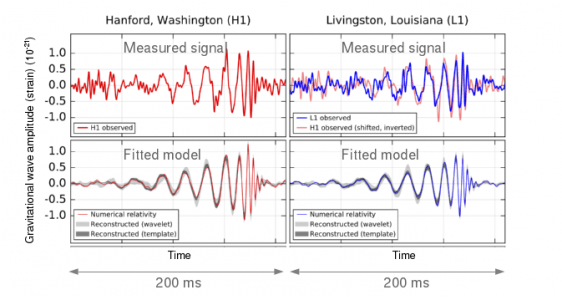
First ever direct detectin of a gravitational wave (Ligo and Virgo collaboration)
Index of the lectures
In blue the parts already covered during the lectures
PART 1: Intro
Newtonian gravity:
1. Newtonian gravity: idea and problems
The equivalence principle:
1. The equivalence principle, gravity ↔ non inertial frames
2. Predictions: gravitational redshift and lensing
More then Newtonian gravity
2. The most general classical non-relativistic gravitational field
3. The link between Φ α r-1 and the Euclidean space
PART 2: flat space-time
Special relativity: Minkowski space-time
1. Special relativity, the need, the idea and the the Lorentz transforms
2. The Lorentz geometry and the Lorentz group
3. Groups, Lie-groups, Lie algebra applied to the Lorentz transformation
4. Relativistic mechanics
Attempting a relativistic linear theory of gravity
1. Dynamic of a particle in the field: perihelion shift problem
2. Relativistic linear theory: dynamic of the field
Approaching general relativity: gravity ↔ non inertial frames
1. Recalling the equivalence principle
2. Non-inertial frames and the equivalence principle: example, a rotating frame
3. Connection between gravity and the metric of space-time
PART 3: curved space-time
Curved space-time
1. Getting formal: scalars, vectors, one-forms and tensors
2. Manifolds, geometry, Riemanian geometry
3. The tangent space
4. Connection and covariant derivatives
5. Torsion
6. Link between the connection and the metric tensor
7. Parallel transport and the geodesic equations
8. Curvature Riemann tensor and Einstein tensor
9. Geodesic deviation equation
10. Conserved quantities, killing vectors and Lie derivatives
11. Strong-equivalence principle; electrodynamics in curved space-time
Field equations
1. The source of gravity: energy momentum tensor
2. Einstein field equations, Einstein's approach
3. Einstein field equations, Hilbert's approach
4. Is there one single theory of gravity?
5. Linearized field equations
6. Nearly Newtonian regime and gravitomagnetic field
PART4: applications
Gravitational waves
1. Gravitational waves
2. Generation of gravitational waves
Spherically symmetric systems
1. Schwartzshild metric
2. Schwartzshild black-holes
4. Kruskal coordinates
5. Reissner-Nordström (electrically charged black-holes)
Axially symmetric systems
1. Kerr metric (rotating spherical objects)
Cosmology: isotropic and homogeneous universe
1. Friedmann(-Lamaitre)-Robertson-Walker metric (FLRW)
2. The cosmological constant and dark energy
Material
Suggested readings
- General Relativity (R. Wald): {https://vdocument.in/robert-m-wald-general-relativity.html}
- - The classical Theory of fields (Landau and Lifshitz Vol.2): {http://fulviofrisone.com/attachments/article/209/Landau%20L.D.%20Lifschitz%20E.M.-%20Vol.%202%20-%20The%20Classical%20Theory%20of%20Fields.pdf}
- - General Relativity: An Introduction for Physicists (M.P. Hobson, G.P. Efstathiou and A.N. Lasenby): {https://ia800108.us.archive.org/26/items/gnsecBooks/%5BM._P._Hobson%2C_G._P._Efstathiou%2C_A._N._Lasenby%5D_Ge%28BookFi%29.pdf}
- Lecture Notes on General Relativity (S.M. Carrol): {https://arxiv.org/abs/gr-qc/9712019}
- Lecture notes Prof. Schaefer
- Lecture notes Prof. Amendola
- Lecture notes Prof. Bartelmann
Videos
- The lectures will be recorder and made available on Youtube: https://www.youtube.com/playlist?list=PLG4KhehRXgYsCJtYYk1A-7-TP-Q_pyFZT
Lecture notes
- 01: Introduction
- 02: Equivalence principle
- 03: Non relativistic linear theory
- 04: Special relativity, the core concept
- 05a: Lorentz geometry
- 05b: Groups (bonus)
- 05c: Lie algebra and the Lorentz group
- 06: Relativistic mechanics
- 07a: perihelion shift, Relativistic linear theory
- 07b: fluids with gravity (bonus)
- 08: Toward GR, linking gravity to the metric
- 09: Vectors, 1-forms and tensors
- 10: Manifolds and the tangent space
- 11: About the tangent space
- 12: Affine connection and covariant derivative
- 13: Parallel transport and geodesic equation
- 14: Curvature tenosr
- 15: Geodesic deviation equation
- 16: Ricci tensor, Ricci scalar and Einstein tensor
- 18: SEP and electrodynamics in curved space
- 19: Energy-Momentum tensor
- 20: Einstein field equations
- 17a: Killing vectors and Killing vector field
- 17b: Lie derivatives and conserved quantities
- 21: Einstein field equations via variational approach
- 22: Not only one Theory of gravity
- 23: Linearized Einstein equations
- 23b: Gauge transformation of the perturbation h (bonus)
- 24: Nearly newtonian regime, gravitomagnetic field
- 25: Gravitational waves
- 26: Generation of gravitational waves
- 27: Spherycal symmetry and Schwarzshild metric
- 28: Motion of particles in Schwarzshild space-time
- 29: Schwarzshild black holes
- 30: Reissner-Nordstroem solution and black holes
- 31: Kerr solution and Kerr back holes
- 32: Relativistic cosmological model
- 33: Conclusions
- GR: all lecture notes merged together with a clicable index
Übungsblätter
- 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
Übungsgruppen
- Gruppe 01 (Adrian Schlosser)
12 Teilnehmer/innen
INF 227 / SR 2.404, Di 09:15 - 11:00 - Gruppe 02 (Shayan Hemmatyar)
12 Teilnehmer/innen
INF 227 / SR 2.403, Di 11:15 - 13:00 - Gruppe 03 (Yannic Pietschke)
13 Teilnehmer/innen
Philos.-weg 12 / R 068, Mi 14:15 - 16:00 - Gruppe 04 (Selin Üstündag)
16 Teilnehmer/innen
Philos.-weg 12 / kHS, Do 09:15 - 11:00 - Gruppe 05 (Carlos Pastor Marcos)
11 Teilnehmer/innen
Philos.-weg 12 / kHS, Do 11:15 - 13:00 - Gruppe 06 (Jiahan Shi)
10 Teilnehmer/innen
Philos.-weg 12 / R 060, Fr 09:15 - 11:00 - Gruppe 07 (Shaun Fell)
10 Teilnehmer/innen
Philos.-weg 12 / R 060, Fr 14:15 - 16:00 - Gruppe 08 (Youssef Aly)
11 Teilnehmer/innen
Philos.-weg 12 / R 070, Di 9:15 - 11:00 - Gruppe 09 (Felix Heinze)
11 Teilnehmer/innen
Philos.-weg 12 / R 056, Fr 14:15 - 16:00 - Gruppe 10 (Quentin Coppee)
10 Teilnehmer/innen
Philos.-weg 12 / R 068, Mi 16:15 - 18:00 - Gruppe 11 (Vito Aberham)
9 Teilnehmer/innen
INF 501 / FP (R. 102), Fr 9:15 - 11:00
