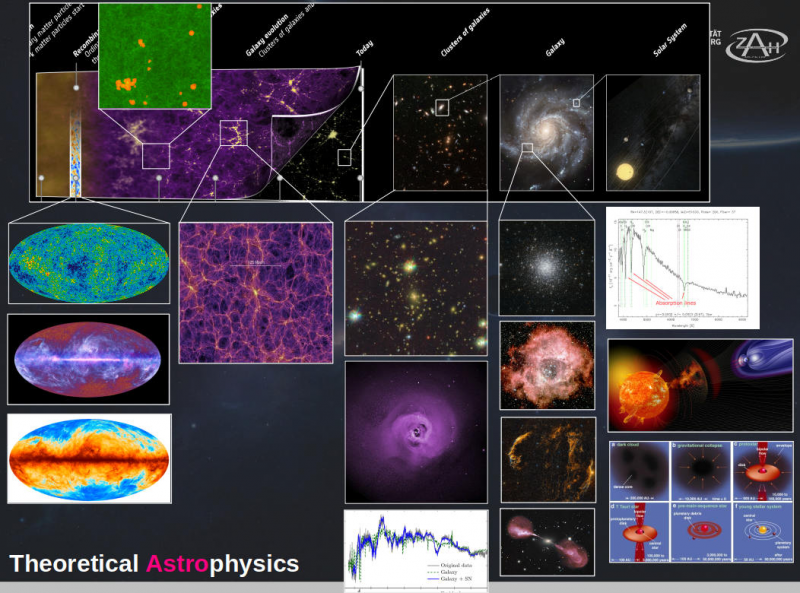
Theoretical Astrophysics
Lecturer:
Priv.-Doz. Dr. Matteo Maturi (ITA/ZAH, ITP)
maturi@uni-heidelberg.de
Head tutor:
Dr. Giulia Despali (ITA)
gdespali@uni-heidelberg.de
Space and time:
- Winter semester, 2022/23
- From 17.10.2021 to 15.02.2023
- Monday 09:15-11:00 (Philosophenweg 12 gHS)
- Wednesday 09:15-11:00 (Philosophenweg 12 gHS)
Overview:
The lectures will cover a variety of topics that will allow the students to understand the physics involving celestial bodies such as planets, stars, nebulae, black holes, galaxies, galaxy clusters, etc.. The lectures and exercise classes are held in English.
Content:
- Basics: recap on basic concepts - A glimpse at cosmology, Special relativity - Electrodynamics - Phase space and Planck spectrum
- Radiation processes: emission and absorbtion in the cosmos - Thompson and Compton scattering - Spectra (in general) and quantum transitions - Synchrotron and Bremsstrahlung - Radiation transport
- Hydrodynamics: how to deal with fluids - Ideal hydrodynamics - Viscous hydrodynamics - Examples and applications - shock waves and instabilities
- Plasma physics: how to deal with ionized gasses - Collisionless plasmas - Radiation in ionized media - Thermal plasmas - Magnitohydrodynamics
- Stellar dynamics: the Jeans equations - The tensor virial theorem
- Gravitational wanders (bonus): New important windows in astrophysics - Gravitational lensing, dark matter mapping and black hole shadows - Gravitational waves and merging of black holes
Prerequisites:
PTP3 and PTP4 are helpful but not mandatory.
The lectures will be held in person.
Important:
To get credit points for the lectures it is necessary to enroll and join one of the tutorial groups. The tutorials will start one week after the main lectures.
To get credit points for the lectures it is necessary to enroll and join one of the tutorial groups. The tutorials will start one week after the main lectures.
Literature:
Theoretical Astrophysics: an Introduction (Matthias Bartelmann)
Radiative processes in Astrophysics (Rybicki & Lightman)
The classical theory of fields: vol. 2 (Landau & Lifshitz)
Weak gravitational lensing (Matthias Bartelmann & Matteo Maturi)
Introduction to cosmology (Matteo Maturi)
Script and exercises:
Additional material and the exercises will be added below and will be available for download.
First exam: February 22nd 2023, 9am in INF 227 HS1
Retake exam: April 13th 2023, 9am in Phil.12 kHS
Retake exam: April 13th 2023, 9am in Phil.12 kHS
Admission to the exam:
1. Attend at least 50% of the tutorials. If attendance < 50%, it is required to hand in 3 full exercise sheets that will be graded.
AND
2. Gain 3 points by:
2. Gain 3 points by:
presenting half exercise (1 point)
actively participating in the discussion during the tutorials (max 1 point per tutorial).
actively participating in the discussion during the tutorials (max 1 point per tutorial).
Lehre, Studium und Forschung:
Lecture Token MKTP2 (8CP): LSF
INDEX OF THE LECTURES:
Introduction - special relativity
01: introduction
02: special relativity, the concept
03: space-time, vectors and one-forms
04a: Lorentz geometry
04b: Lie algebra of the Lorentz group (bonus material)
Behaviour of neutral particles
05: relativistic mechanics
06: particles in a gravitational field, General relativity
Behaviour of Charged particles - E.M. fields - Emission/absorption processes
07: electrodynamics, constructing the theory
08: charged particles in EM fields, Lorentz force, EM tensor
09: electromagnetic field invariants
10: charge density, continuity equation, gauge invariance
11: electromagnetic field equations
12: solution of the field equations
13: energy-momentum tensors (closed systems)
14a: energy-momentum-tensor of electromagnetic fields and Larmor formula
02: special relativity, the concept
03: space-time, vectors and one-forms
04a: Lorentz geometry
04b: Lie algebra of the Lorentz group (bonus material)
Behaviour of neutral particles
05: relativistic mechanics
06: particles in a gravitational field, General relativity
Behaviour of Charged particles - E.M. fields - Emission/absorption processes
07: electrodynamics, constructing the theory
08: charged particles in EM fields, Lorentz force, EM tensor
09: electromagnetic field invariants
10: charge density, continuity equation, gauge invariance
11: electromagnetic field equations
12: solution of the field equations
13: energy-momentum tensors (closed systems)
14a: energy-momentum-tensor of electromagnetic fields and Larmor formula
14b: momentum of intensity
14c: spectrum of radiation
15a: applications Larmor formula: Thomson cross section, Eddington luminosity
15b: applications Larmor formula: synchrotron radiation
15c: applications Larmor formula: bremsstrahlung
15a: applications Larmor formula: Thomson cross section, Eddington luminosity
15b: applications Larmor formula: synchrotron radiation
15c: applications Larmor formula: bremsstrahlung
16: radiation damping
17: photons and Compton scattering
18: phase-space, Planck spectrum
19: astrophysical examples: emission from free charges, scattering, Planck spectrum
20: quantum transitions
21: shape of spectral lines
22: stimulated emission and radiation transport
Behaviour of gas/fluids: hydrodynamics
22: hydrodynamic equations
23: polytropic eq. of state
24: sound waves
25: viscous hydrodynamics
26: evolution of specific entropy
27: vorticity and Raynolds-number
28: Bernoulli's law
29: a deepr look at fluids with gravitational fields
30: transport mechanisms: thermal conduction, convection, tourbolence
31: astrophysical applications: Bondi accreation, self gravitating systems
32: hydrodynamic instabilities
33: shock waves
Behaviour plasma and propagation of light in medium
34: plasma physics
35: electromagnetic waves in media
36: the dielectric tensor and the phase space of particles
37: e.m. waves in thermal plasma
38: magnetohydrodynamics
Stellar dynamics
39: stellar dynamics
Extra (if there is time)
40: dark matter
41: gravitational lensing
42: cosmic microwave background
43: conclusions
17: photons and Compton scattering
18: phase-space, Planck spectrum
19: astrophysical examples: emission from free charges, scattering, Planck spectrum
20: quantum transitions
21: shape of spectral lines
22: stimulated emission and radiation transport
Behaviour of gas/fluids: hydrodynamics
22: hydrodynamic equations
23: polytropic eq. of state
24: sound waves
25: viscous hydrodynamics
26: evolution of specific entropy
27: vorticity and Raynolds-number
28: Bernoulli's law
29: a deepr look at fluids with gravitational fields
30: transport mechanisms: thermal conduction, convection, tourbolence
31: astrophysical applications: Bondi accreation, self gravitating systems
32: hydrodynamic instabilities
33: shock waves
Behaviour plasma and propagation of light in medium
34: plasma physics
35: electromagnetic waves in media
36: the dielectric tensor and the phase space of particles
37: e.m. waves in thermal plasma
38: magnetohydrodynamics
Stellar dynamics
39: stellar dynamics
Extra (if there is time)
40: dark matter
41: gravitational lensing
42: cosmic microwave background
43: conclusions
Lecture notes
- Theoretical Astrophysics WS22/23 all lecture notes
- 01: introduction
- 02: special relativity, the concept
- 03: the space time, vectors and one-forms
- 04a: Lorentz geometry (and the Lorentz group, bonus material)
- 04b: Lie algebra and the Lorentz group (bonus material)
- 05: relativistic mechanics
- 06: a pinch of General Relativity
- 07: electrodynamics, constructing the theory
- 08: charged particles, electro-magnetic field, Lorentz force
- 09: E.M. field tensor components and invariants
- 10: collection of charged particles
- 11: electrodynamics fields equations summary
- 11: electrodynamics fields equations
- 12: solving Maxwell equations
- 13: enery-momentum tensor summary
- 13: enery-momentum tensor
- 14a: enery-momentum tensor of the E.M. field
- 14b: momentum of intensity
- 14c: spectrum of charged particle
- 15a: applications of Larmor-formula: Thomson cross sec. and Eddington luminosity
- 15b: applications of Larmor formula: synchrotron radiation
- 15c: applications of Larmor formula: bremsstrahlung radiation
- 16: radiation damping
- 17: photons, Compton scattering
- 18: the phase-space and the Planck spectrum
- 19: quantum transitions (v2)
- 20: shape of spectral lines
- 21: stimulated emission and radiation transport
- 22: now... what we did so far applied to the universe
- 23: hydrodynamic equations
- 24: polytropic eq. of state
- 25: application, sound waves
- 26: viscous hydrodynamics
- 26b: time evolution of specific entropy
- 27: vorticity and Raynolds number
- 28: Bernoulli constant
- 29: fluids with gravity
- 30: further transport mechanisms
- 31: astrophysical applications
- 32: hydro instabilities
- 33: shock waves
- 34: plasma physics
- 35: electromagnetism in media
- 36a: dielectricity and the phase-space distribution of particles
- 36b: Landau damping
- 36c: E.M. waves in a thermal plasma
- 37: magnito-hydrodynamics
- 38: a pinch of stellar dynamics
Exercise sheets
- Sheet_week1
- Sheet_week_10
- Sheet_week11
- Sheet_week12
- Sheet_week2
- Sheet_week3
- Sheet_week4
- Sheet_week5
- Sheet_week6
- Sheet_week7
- Sheet_week8
- Sheet_week9
Practice groups
- Group Group1 (Giulia Despali)
11 participants
Philos.-weg 12 / R 056, Thu 9:15 - 11:00 - Group Group 2 (Giulio Audagnotto)
11 participants
INF 227 / SR 3.402, Tue 14:15 - 16:00 - Group Group 3 (Yannic Pietschke)
16 participants
INF 227 / SR 2.403, Tue 14:15 - 16:00 - Group Group 4 (Silvia Martocchia)
16 participants
INF 227 / SR 1.403, Thu 14:15 - 16:00 - Group Group 5 (Kilian Höfling)
18 participants
Philos.-weg 12 / R 059, Fri 14:15 - 16:00
